-
林分空间结构体现了林木个体(结构要素)及其属性(分布、种类、大小)的连接方式[1-2],直接反映了林分的生长状态和所处的演替阶段,并间接反映了森林群落生物多样性和生态功能[3-6]。惠刚盈和Gadow[7]系统地提出由参照树及其4株最近相邻木组成的描述林分空间结构的最佳方法,并基于空间结构单元研发了混交度、大小比数、角尺度和密集度4个结构参数[2,6-12]。这4个结构参数精准定位了各林木的自然状态,确切回答了每株树周围最近的4株相邻木有几个比其大或小、如何分布于周围、有多少与其同种、是否相互挤压的问题,既可采用独立均值分析,也可通过联合概率分布即结构参数的N元分布来揭示林木微观结构特征[1,13-14],广泛应用于森林空间结构及林分空间结构多样性分析[15-18]。许多学者将林分空间结构引入林分择伐规则,利用乘除法思想,建立林分择伐空间优化模型[19-21];也有学者直接以林分空间结构为目标函数,以非空间指标为约束,构建林分空间结构评价体系[22-27]。这些研究都是基于空间结构优化的单木经营模型,并不是专门用来比较不同森林类型的林分空间结构的优劣程度。近年来,有研究根据景观生态学中的景观斑块理论,斑块内部要求均质且与邻近斑块有着本质不同特征的原理,把林分作为空间结构研究的基本单位,将斑块均质性理解为林分空间结构的均质性,按照多目标规划的乘除法基本思想,提出了林木均质性指数和林分均质性指数[28-29];也有文献借鉴微观经济学中的柯布-道格拉斯生产函数边际递减效益的思想,基于3个林分空间结构参数(混交度、大小比数和角尺度)构建了以林分空间结构参数为“投入”与林分空间结构为“产出”的林分空间结构生产函数,即林分空间结构指数,并以林分空间结构距离作为描述林分空间结构的综合指标[30];惠刚盈等提出林分状态单位圆方法[14,31],为进行林分空间结构综合评价提供了新方法。林分空间结构参数之间既是相互独立,又是相互联系、相互制约的有机整体,系统整合分析林分水平空间结构的4个方面,将有助于深入探究森林结构的奥秘。基于相邻木关系的4个林分空间结构参数各自反映结构的某一方面,通常以一组由4个参数组成的向量表达,如何将这4个参数的概括统计量如均值整合成一个能反映结构优劣态势的综合指数,是目前林分结构研究亟待解决的科学问题。本研究试图给出林分空间结构的整体表达,旨在为各种森林类型的林分空间结构的绝对比较提供方法,亦为同一林分的空间结构优化中目标函数的构建提供有效途径,同时便于将林分结构作为综合变量来定量分析或模拟结构对功能的影响。
-
共收集到我国4个地区47块样地的林分空间结构参数均值,代表了15种不同森林类型,详见表1。其中,甘肃小陇山的12块样地(样地编号9~20)代表了不同经营模式的林分,依次为锐齿栎(Quercus aliena var. acuteserrata Maxim.)天然阔叶混交林(近原始林)模式,锐齿栎天然阔叶混交林皆伐-人工补植油松(Pinus tabulaeformis Carr.)-自然恢复模式,锐齿栎天然阔叶混交林择伐抚育模式,锐齿栎天然阔叶混交林结构化经营模式,锐齿栎天然阔叶混交林目标树经营模式,天然阔叶林全面改造-人工更新华山松(Pinus armandii Franch.)模式、人工更新油松模式,天然灌木林带状改造-人工更新华山松模式、人工更新油松模式,天然灌木林全面改造-人工更新华山松模式、人工更新油松模式、人工更新日本落叶松(Larix kaempferi(Lamb.)Carr)模式。吉林和甘肃样地概况详见文献[12,32-33];湖南平江样地概况详见文献[34]。
表 1 林分类型及空间结构参数均值汇总
Table 1. Stand types and mean values of spatial structure parameters
样地编号
Plot No.样地位置
Location of sample plot林分起源
Stand origin林分类型
Stand types林分空间结构参数均值
Mean values of spatial structure parameters角尺度
Uniform angle index混交度
Mingling大小比数
Dominance密集度
Crowding1 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.489 0.793 0.490 0.966 2 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.534 0.775 0.488 0.957 3 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.491 0.827 0.492 0.827 4 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.496 0.780 0.490 0.780 5 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.514 0.798 0.487 0.950 6 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.486 0.838 0.494 0.958 7 内蒙红花尔基
Honghuaerji Inner Mongolia天然林
Natural forest樟子松林
Pinus sylvestris var.
mongolica forest0.463 0.494 0.388 8 内蒙红花尔基
Honghuaerji Inner Mongolia天然林
Natural forest樟子松林
Pinus sylvestris var.
mongolica forest0.465 0.496 0.360 9 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.489 0.798 0.494 10 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.520 0.761 0.473 11 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.487 0.656 0.492 12 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.480 0.813 0.496 13 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.522 0.616 0.503 14 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation华山松林
Pinus armandii plantation0.381 0.600 0.384 15 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation油松林
Pinus tabulaeformis plantation0.413 0.484 0.422 16 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation华山松林
Pinus armandii plantation0.514 0.323 0.541 17 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation油松林
Pinus tabulaeformis plantation0.472 0.324 0.523 18 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation华山松林
Pinus armandii plantation0.459 0.347 0.463 19 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation油松林
Pinus tabulaeformis plantation0.431 0.291 0.494 20 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation日本落叶松林
Larix kaempferi plantation0.388 0.291 0.463 21* 湖南平江
Pingjiang Hunan人工林
Plantation杉木、马尾松、柳杉林
Cunninghamia lanceolata、
Pinus massoniana、
Cryptomeria fortunei mixed forest0.350 0.050 22* 湖南平江
Pingjiang Hunan人工林
Plantation木荷
Schima superba Gardn. et Champ.0.280 0.020 23* 湖南平江
Pingjiang Hunan人工林
Plantation7木荷3闽楠混交林
7 Schima superba
3 Phoebe bournei mixed forest0.400 0.470 24* 湖南平江
Pingjiang Hunan人工林
Plantation7柳杉3马褂木
7 Cryptomeria fortunei
3 Liriodendron chinense mixed forest0.390 0.520 25* 湖南平江
Pingjiang Hunan天然林
Natural forest青冈栎混交林
Cyclobalanopsis glauca mixed forest0.490 0.730 *注:样地21和24分别为9块样地均值,样地22、23和25为3块样地均值。
Note:Sample plots 21 and 24 are the mean values of 9 sample plots, sample plots 22, 23 and 25 are the mean values of 3 sample plots. -
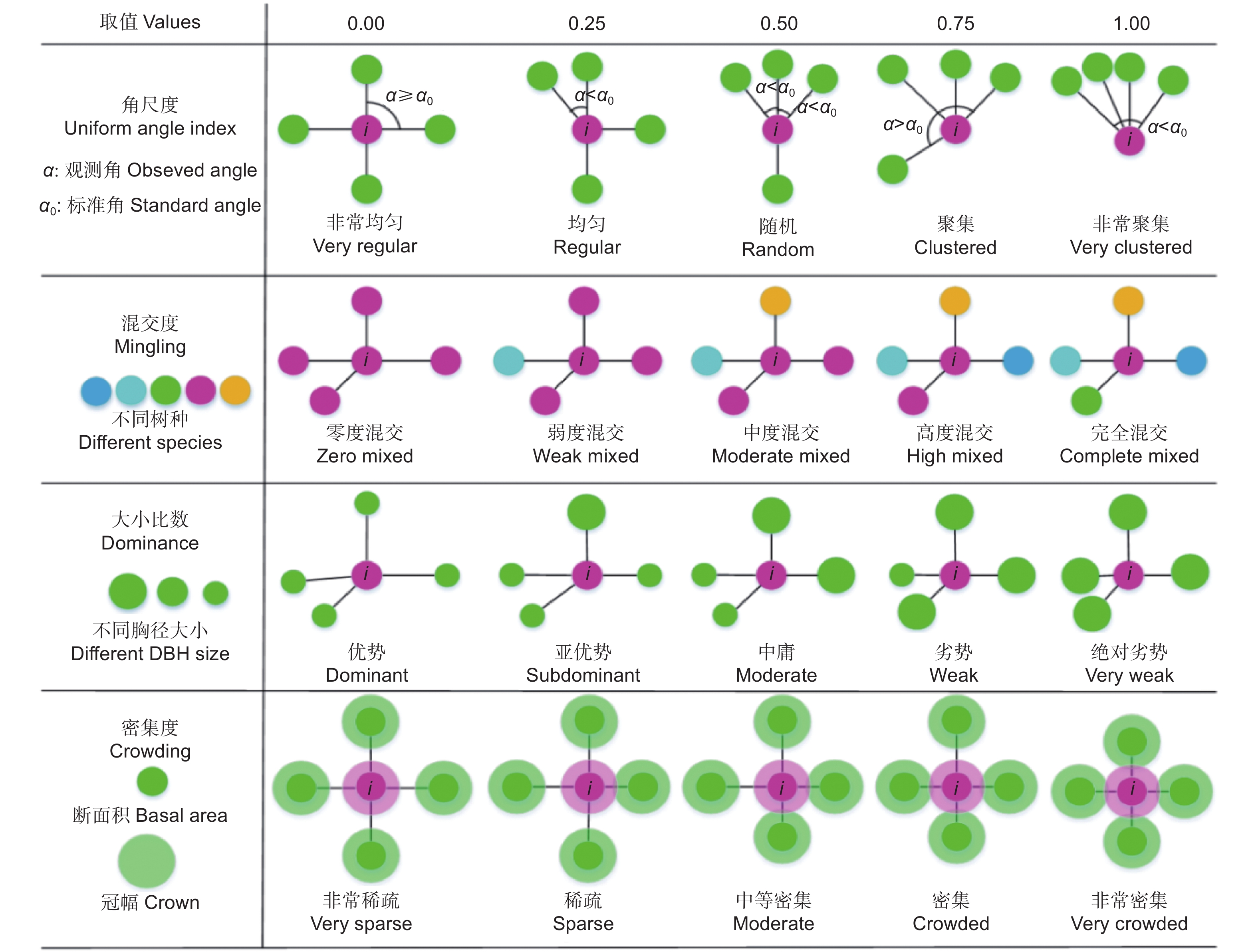
基于林分空间结构单元而建立的由4个空间结构参数构成的参数体系已成为分析林分结构不可分割的有机整体[1]。4个空间结构参数体系(图1),包括描述林木个体在水平分布格局的角尺度、体现树种空间隔离程度的混交度、反映林木个体竞争状态的大小比数和体现林木密集程度的密集度[1]。各参数均值计算方法如下:
林分角尺度均值:
$ {\overline{W}}=\frac{1}{N}\sum _{i=1}^{N}{W}_{i}=\frac{1}{4N}\sum _{i=1}^{N}\sum _{j=1}^{4}{z}_{ij} $
(1) $ {z}_{ij}\left\{ \begin{array}{l}1,当第j个\alpha 角小于标准角{\alpha }_{0}=72^\circ;\\ 0,否则\end{array}\right. $
式(1)中,
$ {\overline{W}} $ 为林分平均角尺度;$ {W}_{i} $ 为第i株树的角尺度;N为样地内消除边缘效应后的有效林木株数。林分混交度均值:
$ {\overline{M}}=\frac{1}{N}\sum _{{i}=1}^{N}{M}_{{i}}=\frac{1}{4N}\sum _{i=1}^{N}\sum _{j=1}^{4}{v}_{ij} $
(2) $ {v}_{ij}\left\{ \begin{array}{l}1,当参照树i与第j个相邻木为不同种时;\\ 0,否则\end{array}\right. $
式(2)中,
$ {\overline{M}} $ 为林分平均混交度;$ {M}_{i} $ 为第i株树的混交度;N为样地内消除边缘效应后的有效林木株数。林分大小比数均值:
$ {\overline{U}}=\frac{1}{N}\sum _{{i}=1}^{N}{U}_{{i}}=\frac{1}{4N}\sum _{i=1}^{N}\sum _{j=1}^{4}{k}_{ij} $
(3) $\begin{aligned} \;\\ {k}_{ij}\left\{ \begin{array}{l}0,当第j个相邻木比参照树i小时;\\ 1,否则\end{array}\right. \end{aligned}$
式(3)中,
$ {\overline{U}} $ 为林分平均大小比数;$ {U}_{i} $ 为第i株树的大小比数;N为样地内消除边缘效应后的有效林木株数。林分密集度均值:
$ {\overline{C}}=\frac{1}{N}\sum _{i=1}^{N}{C}_{i}=\frac{1}{4N}\sum _{i=1}^{N}\sum _{j=1}^{4}{y}_{ij} $
(4) $ {y}_{ij}\left\{ \begin{array}{l}1,当第j个相邻木比参照树i小时;\\ 0,否则\end{array}\right. $
式(4)中,
$ {\overline{C}} $ 为林分平均密集度;$ {C}_{i} $ 为第i株树的密集度;N为样地内消除边缘效应后的有效林木株数。 -
林分空间结构参数角尺度、混交度、大小比数和密集度的均值都是0~1之间的值,显然不需要归一化处理,但这4个结构参数除了混交度外,其它3个指标都不是越大越好。为便于整合结构参数,有必要对这4个结构参数均值进行正向处理(数值越大越好)。
混交度均值为0~1之间的数值,其值越大,表示混交程度越好,树种多样性也高。混交度为正向指标,越大越好。该指标适用于混交林结构的评价,对于极端立地条件下的天然纯林可不考虑混交问题。
角尺度均值是林木分布格局判别的关键指标,如果其值在
$ \left[\mathrm{0.475,0.517}\right] $ 之间,格局则被判定为随机分布。随机分布是天然原始顶级群落最为显著的结构特征,被认为是自然界中最为合理的分布形式,所以,赋值为1;角尺度均值大于0.517为团状分布,符合除顶级群落外的其它天然林类型特征,被认为是较接近合理格局的过渡形式,赋值为0.5;而角尺度均值小于0.475,则判定为均匀分布,被认为是竞争最为激烈的格局,人工林(除飞播造林外)的林木分布格局大都是均匀分布,稳定性差。对于均匀分布的林分来讲,不用再重新赋值,直接采用其林分角尺度均值即可。密集度均值主要体现林木平均拥挤程度。对于单层同龄林而言,它既是对林分空间利用程度的测度,也是评价林分潜在生产力的指标,如果仅仅是林分空间利用程度指标,那自然是越大越好。这个指标如同林分株数密度指标,有其合理密度范围,合理的密集度值应该是既有利于林木个体生长又不造成林分空间浪费。根据密集度定义可知,当其值在0.75时,对应密集度分布区间为
$ \left[\mathrm{0.625,0.875}\right] $ ,对于同龄林而言,最简单直观的理解就是林分中大部分林木3面空间利用充分,还有一面潜在可利用空间,这既有利于单株林木生长,又有利于林分群体生产力形成,赋值为1;而对于复层异龄林而言,由于复层的缘故,水平空间利用较充分,故赋值0.75。当密集度值在0.5时,对应密集度分布区间为$ \left[0.375,\left.0.625\right)\right. $ ,对于单层同龄林而言,最简单直观的理解就是林分中大部分林木2面还有潜在生长空间,虽对林木个体有利,但林分整体空间利用不充分,赋值0.75;而对于复层异龄林,水平空间利用则不充分,赋值0.5。当密集度值在0.25附近,对应密集度分布区间为$ \left[0.125,\left.0.375\right)\right. $ ,对于单层同龄林而言,最简单直观的理解就是林分中大部分林木3面还有潜在生长空间,虽对林木个体有利,但林分整体空间利用非常不充分,赋值0.5;对于复层异龄林,水平空间利用则很不充分,赋值0.25;当密集度均值大于0.875,对于同龄林而言,林分整体太密,赋值0.25;对于复层异龄林而言,水平空间利用很充分,赋值1;林分平均密集度值小于0.125,疏林状态,赋值0。大小比数均值既是林分优势度的评判,更是林木大小分布格局异质性的体现,深度剖析林分大小比数均值的意义必须从其定义出发。在一个孤立的结构单元中,如果5棵树林木互为邻体,按照大小比数的定义,2株林木比较时,
$ {k}_{ij} $ 的均值一定等于(0 + 1)/2=0.5或(1 + 0)/2=0.5,Ui的值一定属于{0,0.25,0.5,0.75,1}中的一个,这个孤立的结构单元的均值一定等于0.5。自然界最常见的是:①林分中林木完全均衡分布,每个等级{0, 0.25, 0.5, 0.75, 1}中频率相等各占20%,②林分中林木不完全均衡分布,各等级频率不完全相等,但有一定规律:如果一个林分中属于0.75或1的等级高于或低于20%,意味着属于0或0.25 等级的林木频率等级也一定高于或低于20%,也就是说,大小比数中值等级0.5两边的等级频率几乎相等,只有这样才能使其均值等于0.5。所以,这里将以上林分称为林木大小分布均衡的林分,但这并不意味着,该林分在某一测度指标上具有优势,最直观的理解应该是该林分的林木大小处于均衡状况,显然具有大小优势的林分一定是大小比数取值中0或0.25等级的林木株数占优,其均值一定小于0.5;相反,林木大小处于劣势的林分一定是大小比数取值中0.75或1等级的林木株数占优。自然界林分中每个林木与其最近4株树组成的结构单元并不都是孤立的,其均值取决于{0, 0.25, 0.5, 0.75, 1}各等级的频率大小,虽然有许多林分的大小比数均值都在0.5附近,但不能认为该林分中林木大小处于中庸状态。所以,这里给出一个判别林分中林木大小格局分布优劣态势的标准,如果大小比数均值在(0.49, 0.51)之间,表示均衡,大小均匀分布,异质性较差,赋值0.5;均值在$ \left[\mathrm{0.47,0.49}\right] $ 时赋值0.75;均值小于0.47时赋值1,表明林分中具有大小优势的林木较多;均值在$ \left[\mathrm{0.51,0.53}\right] $ 时赋值0.25;均值>0.53时赋值0。结构参数均值标准化一览表(表2)。表 2 结构参数均值-标准化值对照
Table 2. Comparison of mean and standardized values of structural parameters
结构参
数均值
Mean values
of structure
parameters混交度$ \overline M $
Mingling角尺度$ \overline W $
Uniform angle index大小比数$ \overline{U} $
Dominance密集度$ \overline C $
Crowding备注
Note<0.475 [0.475,
0.517]>0.517 <0.47 [0.47,
0.49](0.49,
0.51)[0.51,
0.53]>0.53 <0.125 [0.125,
0.375)[0.375,
0.625)[0.625,
0.875]>0.875 标准化值
Standardized
values实测值
Measured
value实测值
Measured
value1.0 0.5 1.0 0.75 0.5 0.25 0.0 0.0 0.5/0.25 0.75/0.5 1.0/0.75 0.25/1.0 单层/
复层
Single
layer/
Multiple
layers -
林分空间结构参数均值经上述标准化处理后,既保持了归一化的简洁特性,同时又具备正向指标越大越好的优点,便于进行综合评价。综合评价有多种方法[14],鉴于单位圆法[14,33]既能直观反映评估对象在各指标上的相对优劣程度,又能比对最优林分状态
$ {\pi} $ 值法则对评价对象作出整体性评价,具有简洁、直观、形象和可操作性强等特点,故本研究采用单位圆法对林分空间结构进行综合评价。基于单位圆法并比对最优林分状态的
$ {\pi} $ 值法则(图2),可构造林分空间结构评价指数,简称为平方均值指数(FSS):$ FSS=\frac{\displaystyle \sum \nolimits_{k=1}^{m}\dfrac{{\pi}{R}_{k}^{2}}{m}}{{\pi}{R}^{2}}=\frac{1}{m}{\sum }_{k=1}^{m}{R}_{k}^{2} $
(5) 式中:m— 结构参数个数;Rk—第k个结构参数正向指标值。
-
利用上述方法,基于表1的原始数据,对非正向指标首先进行正向处理,然后用公式(1)进行计算,结果见表3。
表 3 林分空间结构参数综合评价
Table 3. Comprehensive evaluation of spatial structure parameters of forest stands
编号 No. 林分空间结构参数均值/正向处理结果 Results of mean/positive treatment of spatial structure parameters 角尺度 Uniform angle index 混交度 Mingling 大小比数 Dominance 密集度 Crowding 平方均值指数 FSS 单位圆 Unit circle 1 0.489/1.000 0.793/0.793 0.490/0.75 0.966/1.00 0.798 
2 0.534/0.500 0.775/0.775 0.488/0.75 0.957/1.00 0.603 
3 0.491/1.000 0.827/0.827 0.492/0.50 0.827/0.75 0.624 
4 0.496/1.000 0.780/0.780 0.490/0.75 0.780/0.75 0.683 
5 0.514/1.000 0.798/0.798 0.487/0.75 0.950/1.00 0.800 
6 0.486/1.000 0.838/0.838 0.494/0.50 0.958/1.00 0.738 
7 0.463/0.463 0.494/0.50 0.388/0.50 0.238 
8 0.465/0.465 0.496/0.50 0.360/0.25 0.176 
9 0.489/1.000 0.798/0.798 0.494/0.50 0.629 
10 0.520/0.500 0.761/0.761 0.473/0.75 0.464 
11 0.487/1.000 0.656/0.656 0.492/0.50 0.560 
12 0.480/1.000 0.813/0.813 0.496/0.50 0.637 
13 0.522/0.500 0.616/0.616 0.503/0.50 0.293 
14 0.381/0.381 0.600/0.600 0.384/1.00 0.502 
15 0.413/0.413 0.484/0.484 0.422/1.00 0.468 
16 0.514/1.000 0.323/0.323 0.541/0.00 0.368 
17 0.472/0.472 0.324/0.324 0.523/0.25 0.130 
18 0.459/0.459 0.347/0.347 0.463/1.00 0.444 
19 0.431/0.431 0.291/0.291 0.494/0.50 0.173 
20 0.388/0.388 0.291/0.291 0.463/1.00 0.412 
21 0.350/0.350 0.050/0.050 0.063 
22 0.280/0.280 0.020/0.020 0.039 
23 0.400/0.400 0.470/0.470 0.190 
24 0.390/0.390 0.520/0.520 0.211 
25 0.490/1.000 0.730/0.730 0.766 
由表3可见,经标准化处理后的各结构参数指标范围更大,最大值可以达到1.0水平,最小值因结构参数不同有所不同,其中,角尺度最小值与处理前相同,密集度指标最小值为0.25,而大小比数最小值可达最低水平0.0,人们可以根据处理后的各指标值大小直观判断出林分在某一尺度上的优劣态势。
综合评价指数全面给出了林分空间结构的综合态势。FSS指数表明:1)天然林中极端立地条件下的天然纯林空间结构最差;2)天然混交林的空间结构优于人工混交林;3)人工林中人工混交林的林分空间结构明显优于人工纯林; 4)天然纯林空间结构优于人工纯林,主要原因是人工纯林林木分布格局比天然纯林更均匀;以上4点与目前的科学认知一致[12,35-39];5)在甘肃小陇山11种森林经营模式中,结构化经营最好,非常接近原始林的林分空间结构,这与袁士云[40]从经营模式的生产可行性和技术先进性综合评价结果一致。研究结果与前人的研究或普遍的认知相同,意味着研究方法的合理性。
所构建的林分空间结构综合评价指数FSS可以用单位圆方式展示,更直观(表3,单位圆)。人们可以从单位圆深色图形面积大小
$ FSS\times {\pi} $ 直接获知林分结构优劣,譬如,本研究中面积最大的前3位依次是,吉林阔叶红松林5号样地(面积为$ FSS\times {\pi}=0.8\times {\pi}\approx 2.513 $ ),吉林阔叶红松林1号样地(面积为$ FSS\times {\pi}=0.798\times {\pi}\approx 2.507 $ ),湖南青冈栎天然次生林25号样地(面积为$ FSS\times {\pi}=0.766\times {\pi}\approx 2.406 $ )。显然,这与基于最优林分结构$ {\pi} $ 值相比而获得的FSS的值的排序完全相同。 -
与现有的距离方法[21,30]相比,本研究提出的基于
$ {\pi} $ 值法则的平方均值指数更精准。该指数不仅体现了各项指标的累加性[14],更体现了林分整体状态的均衡性,这归功于单位圆法中最优林分状态的已知性[33]。现有距离方法中通常包含像角尺度均值越接近0.5越好,即表达形式中包含$ \left|\overline{W}-0.5\right| $ 或($ \overline{W}-0.5 $ )2,显然,一个绝对值或平方值包含了多种情况,且有可能给予完全不同格局类型相同的值,如$ \left|\overline{W}-0.5\right|=0.05 $ ,可能使$ \overline{W} $ =0.55(聚集分布)等同于$ \overline{W}=0.45 $ (均匀分布)。本研究提出的新方法则更注重格局性质,能清楚区分出不同结构类型,视$ \overline{W} $ 值的大小按照角尺度分布区间[10]分别赋以不同的值,即如果$ \overline{W} > 0.517 $ ,表示聚集分布,赋值0.5;$ \overline{W} $ 值在$ \left[\mathrm{0.475,0.517}\right] $ 之间,表示随机分布,赋值1;而$ \overline{W} < 0.517 $ ,则表示均匀分布,直接采用其值参与计算,更能体现不同均匀程度的影响,比传统的赋予均匀分布值为0更合理[41-42],道理很简单,均匀分布的范围很广,就角尺度均值而言,其值可以是区间$ \left[0,\left.0.475\right)\right. $ 中的任何一个数。而这个区间体现了不同发育阶段的人工林格局类型。如,规则造林形成的人工林,期初林木分布格局的角尺度均值大多接近0,但随着林分生长过程中自然稀疏的发生或疏伐干涉,林木格局分布趋于随机[43],角尺度均值自然会逐渐变大[44]。对于大小比数均值而言,其均值取决于{0,0.25,0.5,0.75,1}各等级的频率大小。大小比数均值等于(0.49,0.51),最直观的理解应该是该林分的林木大小处于均衡状况。显然,具有大小优势的林分一定是大小比数取值中0或0.25等级的林木株数占优,其均值一定小于均衡状态的值;对于林分密集度均值而言,标准化的关键是依据单层林与复层林的空间利用,分别赋予不同的值。林分空间结构作为森林结构最直接的表现和最有可能的调控因子[20,26],在很大程度上决定了森林发展的状态、林分稳定性和经营空间的大小[31]。已经成为森林结构研究的热点和森林经营管理的重要内容。本研究中将新构造的林分空间综合指数与单位圆结合,不仅可以直观地反映结构优劣态势,而且可指导林分空间结构优化,特别是对林分空间结构优化方向的确定。例如在6块红松阔叶天然林中,林木的分布格局大多为随机分布的格局,密集度大多处于合理的范围,混交度则处于较高的水平,而大小比数则有4块样地赋值为0.75,2块样地赋值0.5,因此,对于红松阔叶林来说,进行空间结构的优化的方向则是要提高培育对象的竞争优势,即提高顶极树种或主要伴生树种的竞争优势,提高具有大小优势林木的比例。对人工林或不同经营模式的林分来说(如样地14~20),它们的林木分布格局大多是均匀分布格局,混交度较低,林木大小分布均衡,因此经营的方向应该是调整林木的分布格局,通过天然更新或人工促进更新,提高林分树种的混交程度。在确定经营方向后,则可以应用结构化森林经营方法,对林分进行结构优化调整。此外,该综合指数同样可以直接评价林分结构优化调整效果,通过比较经营设计前后空间结构参数变化,结合单位圆面积变化,可直观地了解作业设计是否符合经营方向,有针对性地指导作业设计调整,从而有效避免作业设计不当而造成损失。
-
(1)提出了基于结构参数均值的林分空间结构综合评价方法,构造了基于单位圆
$ {\pi} $ 值法则的林分空间结构综合评价指数,简称平方均值指数(FSS)。典型林分数据验证结果充分表明,所构建的平方均值指数能科学表达出“天然混交林的空间结构优于人工混交林、人工混交林优于人工纯林以及天然纯林优于人工纯林”的普遍认知。(2)对林分空间结构参数均值的意义进行了科学诠释,对其不同取值重新赋值,并进行标准化处理,以此为基础构建了林分空间结构综合评价指数。该指数能够很好地表达林分空间结构的优劣,对林分空间结构优化和效果评价具有很好的指导意义。
基于结构参数均值的林分空间结构综合评价研究
Comprehensive Evaluation of Forest Spatial Structure Based on the Mean Values of Structural Parameters
-
摘要:
目的 构建基于相邻木关系的林分空间结构综合指数用以评价林分空间结构优劣,指导林分结构优化。 方法 在诠释林分空间结构参数角尺度、密集度、大小比数和混交度均值意义的基础上,对林分角尺度、密集度和大小比数的均值重新赋值,进行标准化处理,使其成为正向指标;林分平均混交度为正向指标,采用实测值,然后将林分空间结构参数与单位圆法相结合,构建林分空间结构综合评价指数(FSS),并采用不同林分类型对其有效性进行验证。 结果 运用构建的空间结构综合评价指数对我国4个地区47块样地的评价结果表明:1)天然林中极端立地条件下的天然纯林空间结构最差;2)天然混交林的空间结构优于人工混交林;3)人工林中人工混交林的林分空间结构明显优于人工纯林; 4)天然纯林空间结构优于人工纯林。 结论 构建的林分空间结构综合评价指数能够评价林分空间结构优劣,科学表达出“天然混交林的空间结构优于人工混交林、人工混交林优于人工纯林以及天然纯林优于人工纯林”的普遍认知,是一个良好的林分空间结构综合测度指数,对林分空间结构优化和效果评价具有很好的指导意义。 Abstract:Objective A comprehensive index of stand spatial structure based on adjacent trees was constructed to evaluate the advantages and disadvantages of stand spatial structure and guide the optimization of stand structure. Method Based on the interpretation of the mean values of stand spatial structure parameters of uniform angle index, crowding, neighborhood comparison and mingling, they were assigned and standardized to make them positive indicators; the average value of mingling is a positive index, and the measured value is adopted; Then the stand spatial structure parameters were combined with the unit circle method to construct the stand spatial structure comprehensive evaluation index (FSS), and its effectiveness was verified by different stand types. Result The evaluation results of 47 sample plots in 4 regions of China using the constructed spatial structure comprehensive evaluation index showed that: 1) The spatial structure of natural pure forests under extreme site conditions was the worst among natural forests; 2) The spatial structure of natural mixed forest was better than that of artificial mixed forest; 3) The stand spatial structure of mixed plantation is obviously better than that of pure plantation; 4) The spatial structure of natural pure forest was better than that of artificial pure forest. Conclusion The comprehensive evaluation index of stand spatial structure can evaluate the advantages and disadvantages of stand spatial structure, and can scientifically express the general understanding that "the spatial structure of natural mixed forest is superior to that of artificial mixed forest, artificial mixed forest is superior to that of artificial pure forest, and natural pure forest is superior to that of artificial pure forest". It is a better comprehensive measure index of stand spatial structure, and has guiding significance for optimization of stand spatial structure and effect evaluation. -
表 1 林分类型及空间结构参数均值汇总
Table 1. Stand types and mean values of spatial structure parameters
样地编号
Plot No.样地位置
Location of sample plot林分起源
Stand origin林分类型
Stand types林分空间结构参数均值
Mean values of spatial structure parameters角尺度
Uniform angle index混交度
Mingling大小比数
Dominance密集度
Crowding1 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.489 0.793 0.490 0.966 2 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.534 0.775 0.488 0.957 3 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.491 0.827 0.492 0.827 4 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.496 0.780 0.490 0.780 5 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.514 0.798 0.487 0.950 6 吉林蛟河
Jiaohe Jinlin天然林
Natural forest红松阔叶林
Coniferous-broad leaved
Korean pine mixed forest0.486 0.838 0.494 0.958 7 内蒙红花尔基
Honghuaerji Inner Mongolia天然林
Natural forest樟子松林
Pinus sylvestris var.
mongolica forest0.463 0.494 0.388 8 内蒙红花尔基
Honghuaerji Inner Mongolia天然林
Natural forest樟子松林
Pinus sylvestris var.
mongolica forest0.465 0.496 0.360 9 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.489 0.798 0.494 10 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.520 0.761 0.473 11 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.487 0.656 0.492 12 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.480 0.813 0.496 13 甘肃小陇山
Xiaolongshan Gansu天然林
Natural forest松栎混交林
Pine-oak mixed forest0.522 0.616 0.503 14 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation华山松林
Pinus armandii plantation0.381 0.600 0.384 15 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation油松林
Pinus tabulaeformis plantation0.413 0.484 0.422 16 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation华山松林
Pinus armandii plantation0.514 0.323 0.541 17 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation油松林
Pinus tabulaeformis plantation0.472 0.324 0.523 18 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation华山松林
Pinus armandii plantation0.459 0.347 0.463 19 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation油松林
Pinus tabulaeformis plantation0.431 0.291 0.494 20 甘肃小陇山
Xiaolongshan Gansu人工林
Plantation日本落叶松林
Larix kaempferi plantation0.388 0.291 0.463 21* 湖南平江
Pingjiang Hunan人工林
Plantation杉木、马尾松、柳杉林
Cunninghamia lanceolata、
Pinus massoniana、
Cryptomeria fortunei mixed forest0.350 0.050 22* 湖南平江
Pingjiang Hunan人工林
Plantation木荷
Schima superba Gardn. et Champ.0.280 0.020 23* 湖南平江
Pingjiang Hunan人工林
Plantation7木荷3闽楠混交林
7 Schima superba
3 Phoebe bournei mixed forest0.400 0.470 24* 湖南平江
Pingjiang Hunan人工林
Plantation7柳杉3马褂木
7 Cryptomeria fortunei
3 Liriodendron chinense mixed forest0.390 0.520 25* 湖南平江
Pingjiang Hunan天然林
Natural forest青冈栎混交林
Cyclobalanopsis glauca mixed forest0.490 0.730 *注:样地21和24分别为9块样地均值,样地22、23和25为3块样地均值。
Note:Sample plots 21 and 24 are the mean values of 9 sample plots, sample plots 22, 23 and 25 are the mean values of 3 sample plots.表 2 结构参数均值-标准化值对照
Table 2. Comparison of mean and standardized values of structural parameters
结构参
数均值
Mean values
of structure
parameters混交度$ \overline M $
Mingling角尺度$ \overline W $
Uniform angle index大小比数$ \overline{U} $
Dominance密集度$ \overline C $
Crowding备注
Note<0.475 [0.475,
0.517]>0.517 <0.47 [0.47,
0.49](0.49,
0.51)[0.51,
0.53]>0.53 <0.125 [0.125,
0.375)[0.375,
0.625)[0.625,
0.875]>0.875 标准化值
Standardized
values实测值
Measured
value实测值
Measured
value1.0 0.5 1.0 0.75 0.5 0.25 0.0 0.0 0.5/0.25 0.75/0.5 1.0/0.75 0.25/1.0 单层/
复层
Single
layer/
Multiple
layers表 3 林分空间结构参数综合评价
Table 3. Comprehensive evaluation of spatial structure parameters of forest stands
编号 No. 林分空间结构参数均值/正向处理结果 Results of mean/positive treatment of spatial structure parameters 角尺度 Uniform angle index 混交度 Mingling 大小比数 Dominance 密集度 Crowding 平方均值指数 FSS 单位圆 Unit circle 1 0.489/1.000 0.793/0.793 0.490/0.75 0.966/1.00 0.798 
2 0.534/0.500 0.775/0.775 0.488/0.75 0.957/1.00 0.603 
3 0.491/1.000 0.827/0.827 0.492/0.50 0.827/0.75 0.624 
4 0.496/1.000 0.780/0.780 0.490/0.75 0.780/0.75 0.683 
5 0.514/1.000 0.798/0.798 0.487/0.75 0.950/1.00 0.800 
6 0.486/1.000 0.838/0.838 0.494/0.50 0.958/1.00 0.738 
7 0.463/0.463 0.494/0.50 0.388/0.50 0.238 
8 0.465/0.465 0.496/0.50 0.360/0.25 0.176 
9 0.489/1.000 0.798/0.798 0.494/0.50 0.629 
10 0.520/0.500 0.761/0.761 0.473/0.75 0.464 
11 0.487/1.000 0.656/0.656 0.492/0.50 0.560 
12 0.480/1.000 0.813/0.813 0.496/0.50 0.637 
13 0.522/0.500 0.616/0.616 0.503/0.50 0.293 
14 0.381/0.381 0.600/0.600 0.384/1.00 0.502 
15 0.413/0.413 0.484/0.484 0.422/1.00 0.468 
16 0.514/1.000 0.323/0.323 0.541/0.00 0.368 
17 0.472/0.472 0.324/0.324 0.523/0.25 0.130 
18 0.459/0.459 0.347/0.347 0.463/1.00 0.444 
19 0.431/0.431 0.291/0.291 0.494/0.50 0.173 
20 0.388/0.388 0.291/0.291 0.463/1.00 0.412 
21 0.350/0.350 0.050/0.050 0.063 
22 0.280/0.280 0.020/0.020 0.039 
23 0.400/0.400 0.470/0.470 0.190 
24 0.390/0.390 0.520/0.520 0.211 
25 0.490/1.000 0.730/0.730 0.766 
-
[1] 惠刚盈. 基于相邻木关系的林分空间结构参数应用研究[J]. 北京林业大学学报, 2013, 35(4):1-9. doi: 10.13332/j.1000-1522.2013.04.015 [2] 惠刚盈, 赵中华, 陈明辉. 描述森林结构的重要变量[J]. 温带林业研究, 2020, 3(1):14-20. doi: 10.3969/j.issn.2096-4900.2020.01.003 [3] Brockerhoff E, Jactel H, Parrotta J, et al. Plantation forests and biodiversity: Oxymoron or opportunity?[J] Biodiversity and Conservation. 2008. 17: 925–951. [4] Brockerhoff E G, Barbaro L, Castagneyrol B, et al. Forest biodiversity, ecosystem functioning and the provision of ecosystem services[J]. Biodiversity and Conservation, 2017, 26(13): 3005-3035. doi: 10.1007/s10531-017-1453-2 [5] Ali A. Forest stand structure and functioning: Current knowledge and future challenges[J]. Ecological Informatics, 2019, 98: 665-677. [6] Pommerening A, Zhang G, Zhang X. Unravelling the mechanisms of spatial correlation between species and size diversity in forest ecosystems[J]. Ecological Indicators., 2021, 121: 106995. doi: 10.1016/j.ecolind.2020.106995 [7] 惠刚盈, Klaus von Gadow, Matthias Alber. 一个新的林分空间结构参数——大小比数[J]. 林业科学研究, 1999, 12(1):1-6. [8] 惠刚盈, 胡艳波. 混交林树种空间隔离程度表达方式的研究[J]. 林业科学研究, 2001, 14(1):23-27. [9] 惠刚盈, K. v. Gadow, 胡艳波. 林分空间结构参数角尺度的标准角选择[J]. 林业科学研究, 2004, 17(6): 687-692. [10] 惠刚盈, 克劳斯·冯佳多. 森林空间结构量化分析方法[M]. 北京: 中国科学技术出版社, 2003. [11] 惠刚盈, 张连金, 胡艳波, 等. 林分拥挤度及其应用[J]. 北京林业大学学报, 2016, 38(10):1-6. [12] 惠刚盈, 等. 结构化森林经营理论与实践[M]. 北京: 科学出版社, 2020 [13] Li Y F, Hui G Y, Zhao Z H, et al. The bivariate distribution characteristics of spatial structure in natural Korean pine broad-leaved forest[J]. Journal of Vegetation Science, 2012, 23(6): 1180-1190. doi: 10.1111/j.1654-1103.2012.01431.x [14] 张岗岗, 惠刚盈. 基于累加性和均衡性的林分质量综合评价方法[J]. 林业科学, 2021, 57(1):77-84. doi: 10.11707/j.1001-7488.20210108 [15] Forrester D I, Bauhus J. A review of processes behind diversity-productivity relationships in forests[J]. Current Forestry Reports, 2016, 2(1): 45-61. doi: 10.1007/s40725-016-0031-2 [16] Zhang G, Hui G, Zhang G, et al. Telescope method for characterizing the spatial structure of a pine –oak mixed forest in the Xiaolong Mountains, China[J]. Scand J Forest Res, 2019, 34(6): 1-12. doi: 10.1080/02827581.2019.1680729 [17] Pommerening A, Grabarnik P. Individual-based Methods in Forest Ecology and Management[M]. Springer International Publishing, 2019. [18] Zhao Z H, Hui G Y, Liu W Z, et al. A novel method for calculating stand structural diversity based on the relationship of adjacent trees[J]. Forests, 2022, 13: 343. doi: 10.3390/f13020343 [19] 汤孟平. 森林空间结构分析与优化经营模型研究[D]. 北京: 北京林业大学, 2003. [20] 汤孟平, 唐守正, 雷相东, 等. 林分择伐空间结构优化模型研究[J]. 林业科学, 2004, 40(5):25-31. doi: 10.3321/j.issn:1001-7488.2004.05.004 [21] 李建军, 李际平, 刘素青, 等. 红树林空间结构均质性指数[J]. 林业科学, 2010, 46(6):6-14. doi: 10.11707/j.1001-7488.20100602 [22] 惠刚盈, 李 丽, 赵中华, 等. 林木空间分布格局分析方法[J]. 生态学报, 2007, 27(11):4717-4728. doi: 10.3321/j.issn:1000-0933.2007.11.040 [23] 胡艳波, 惠刚盈. 优化林分空间结构的森林经营方法探讨[J]. 林业科学研究, 2006, 19(1):1-8. doi: 10.3321/j.issn:1001-1498.2006.01.001 [24] 胡艳波. 基于结构化森林经营的天然异龄林空间优化经营模型研究[D]. 北京: 中国林业科学研究院, 2010. [25] 张弓乔. 基于林分状态的试验设计与经营优化[D]. 北京: 中国林业科学研究院, 2015. [26] 曹小玉, 李际平, 封 尧, 等. 杉木生态公益林林分空间结构分析及评价[J]. 林业科学, 2015, 51(7):37-48. [27] Dong L B, Bettinger P, Liu Z G. Optimizing neighborhood-based stand spatial structure: four cases of boreal forests[J]. Forest Econology and Management, 2022, 506: 119965. doi: 10.1016/j.foreco.2021.119965 [28] 李建军, 张会儒, 刘 帅, 等. 基于改进PSO的洞庭湖水源涵养林空间优化模型[J]. 生态学报, 2013, 33(13):4031-4040. [29] 张 江. 森林健康经营空间途径与评价系统研究[D]. 长沙: 中南林业科技大学, 2014. [30] 董灵波, 刘兆刚, 马 妍, 等. 天然林林分空间结构综合指数的研究[J]. 北京林业大学学报, 2013, 35(1):16-22. [31] 惠刚盈, 克劳斯·冯佳多, 等. 结构化森林经营原理[M]. 北京: 中国林业出版社, 2016. [32] 惠刚盈, 等. 森林经营模式评价方法[M]. 北京: 科学出版社, 2012. [33] 惠刚盈, 张弓乔, 赵中华, 等. 天然混交林最优林分状态的π值法则[J]. 林业科学, 2016, 52(5):1-8. [34] 曹小玉, 李际平, 委 霞. 中亚热带典型林分空间结构对土壤养分含量的影响[J]. 林业科学, 2020, 56(1):20-27. doi: 10.11707/j.1001-7488.20200103 [35] Zenner E. Do residual trees increase structural complexity in pacific northwest coniferous forests?[J] Ecological Applications, 2000, 10: 800-810 [36] Puettmann K, Messier C, Coates K. A critique of silviculture: managing for complexity[M]. Washington DC: Island Press. 2008. [37] Messier C, Puettmann K, Coates D. Managing Forests as Complex Adaptive Systems: Building Resilience to the Challenge of Global Change[M]. Routledge, 2013. [38] Liang J, Crowther T, Picard N, et al. Positive biodiversity-productivity relationship predominant in global forests[J]. Science, 2016, 362(6410): 80-83. [39] Huang Y, Chen Y, Nadia C, et al. Impacts of species richness on productivity in a large-scale subtropical forest experiment[J]. Science, 2018, 362(6410): 80-83. doi: 10.1126/science.aat6405 [40] 袁士云. 甘肃省小陇山现有林分经营模式评价研究[D]. 北京: 中国林业科学研究院 2010. , [41] Zhang G Q, Hui G Y, Hu Y B, et al. Designing near-natural planting patterns for plantation forests in China[J]. Forest Ecosystems., 2019, 6(3): 60-72. [42] 刘文桢, 袁一超, 张连金, 等. 基于林分内部状态与邻域环境的油松林稳定性评价[J]. 林业科学, 2021, 57(9):76-86. doi: 10.11707/j.1001-7488.20210908 [43] Pretzsch H. Modellierung des Waldwachstums[D]. Parey Buchverlag Berlin. 2001, 341. [44] 惠刚盈, 赵中华, 胡艳波, 等. 基于角尺度的随机体在森林稳定性维持中的作用[J]. 林业科学, 2021, 57(2):22-30. doi: 10.11707/j.1001-7488.20210203 -
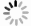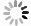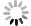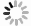



 下载:
下载: