-
反演森林树木高度可以更好地了解森林在全球环境变化中的作用[1-3]。现在,遥感是在区域或全球尺度上进行森林高度反演的最有效方法[4]。极化干涉SAR(PolInSAR)不但拥有微波遥感全天时、全天候的特点,也综合了极化和干涉技术对散射体高度、形状等信息敏感的优点,利用极化干涉SAR技术反演森林树高已经成为林业研究的热点之一[5-6]。
近十年来,RVoG模型一直是树高反演和生物量估计中最常用的模型[7]。2001年,Cloude利用六维非线性优化方法成功反演出植被高度[8],但该方法受初值影响较大且难以求得全局最优解;2003年,Clode基于RVoG (Random Volume over Ground)模型的相干系数在复平面单位圆分布的特点提出了三阶段算法[9];但是,三阶段算法中体散射复相干估计不准确会影响反演精度[10-11]。而对于重复观测或星载极化SAR系统,时间去相关成为主要的误差源[12]。Mette等[13]在研究RVoG模型反演植被高度的3种误差源时,发现时间去相关会导致反演结果产生巨大误差。因此,研究时间去相关问题需要改进RVoG模型或提出新的反演模型。Lee等利用L和P波段SAR数据研究不同时间间隔的时间去相关时发现,时间去相关不仅降低了相干系数,并且增大了植被区相干相位的波动性[14-16]。2003年,Papathanassiou和Cloude[17]提出RVoG+VTD (Random Volume over Ground with Volume Temporal Decorrelation)模型用于解决时间去相关问题,但该模型对反演精度的提升有限。周勇胜等[18]在RVoG+VTD模型的基础上,利用双基线极化干涉SAR数据解决消光系数与植被高度模糊的问题,但只使用模拟数据验证,缺少说服力。2010年,Lavalle提出新的时间去相关模型——TD+RVoG(Temporal Decorrelation Random Volume over Ground)模型[19-21],该模型将时间去相关的原因归结于植被层和地面层的随机高斯运动,但该模型未知数过多,在实际中难以应用。随后,Lavalle提出RMoG(Random Motion over Ground)模型,该模型在TD+RVoG模型的基础上继续发展并利用十维非线性优化方法求解[22],然而这种方法和六维非线性优化方法有同样的缺点且耗时过长;2018年,Nafiseh改进了RMoG模型,提出了RMoGL模型,该模型改用傅里叶-勒让德级数作为结构函数,但该模型的迭代过程比较繁琐、耗时过长,其反演时间大概为RMoG模型的两倍[7]。
可以看出,消除时间去相关的办法是在反演模型中加入植被运动,然而这样就一定要引入更多的未知数,从而使问题变得复杂难解;为了改善RMoG模型反演困难且耗时过长的问题,本研究提出简化RMoG模型,在有效弥补时间去相关的前提下,提高反演效率。为验证该方法,利用欧空局提供的BioSAR2007P波段数据进行试验分析,结果表明,该方法简单高效。
-
研究区位于瑞典南部的Remingstorp地区(58°28′40″ N, 13°37′25″ E),该地区地形相对平坦,总面积超过1 500 hm2,其中大约1 200 hm2为森林,其余为湖泊,海拔高度为120~145 m,树高在10 m到30 m之间,主要树种为挪威云杉(Picea abies (L.) Karst.),欧洲赤松(Pinus sylvestris Linn.)和桦树(Betula spp.),主要土壤类型为耕地土壤。
-
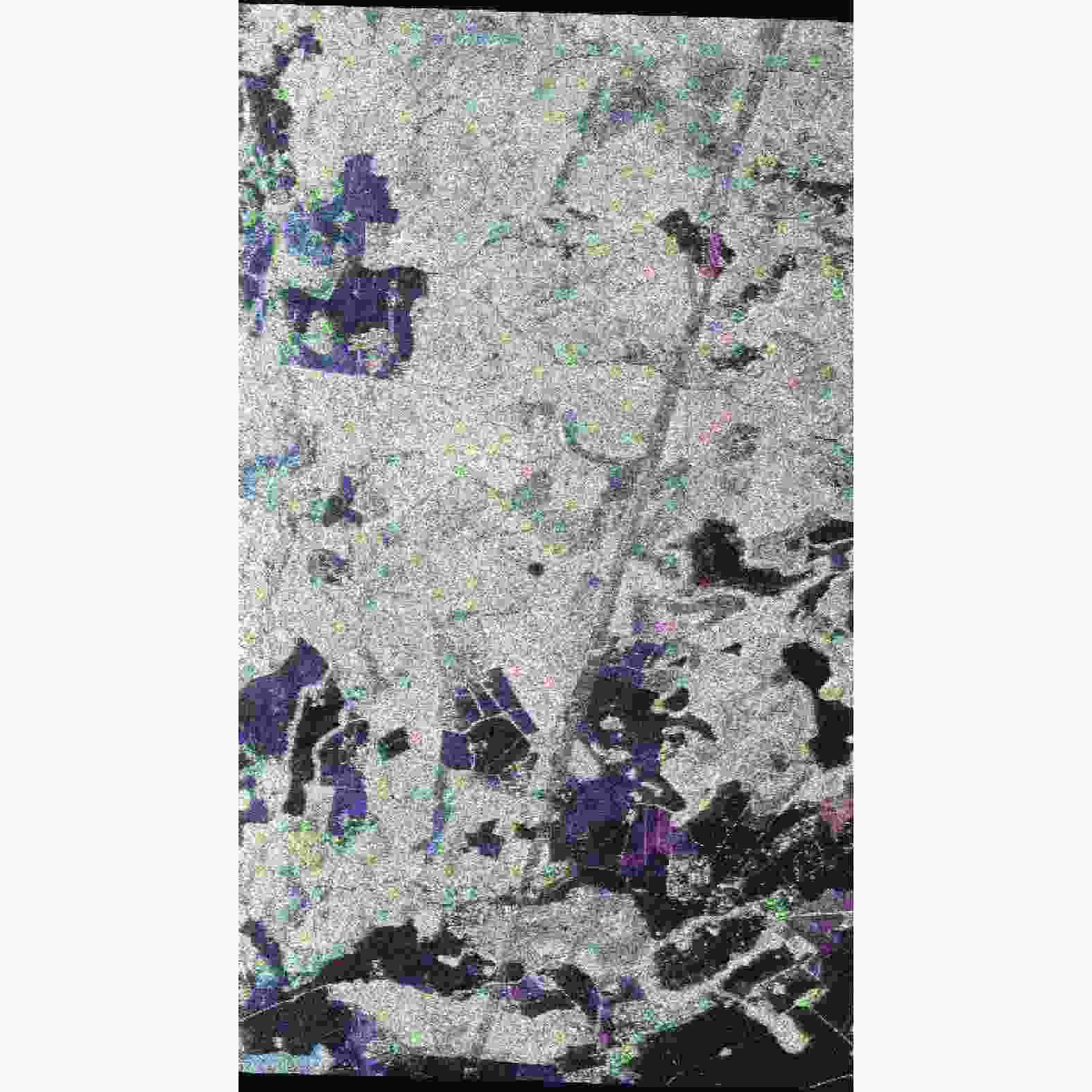
本研究所用的SAR数据是德国宇航局(DLR)与瑞典国防研究局(FOI)利用机载E-SAR系统于2007年获取的P波段全极化干涉数据,其水平基线为40 m,波长为0.86 m,空间基线为20 m,时间基线为50分,距离向分辨率为0.75 m,方位向分辨率1.5 m,数据获取的具体时间为2007年4月2日。数据的主辅影像已经过精确配准,相应的地平数据和有效波数也由DLR提供。为了提高相干性和减弱噪声的影响,数据在预处理时使用了7×7的Boxcar滤波处理。图1为该数据Pauli基下RGB彩色合成图。
-
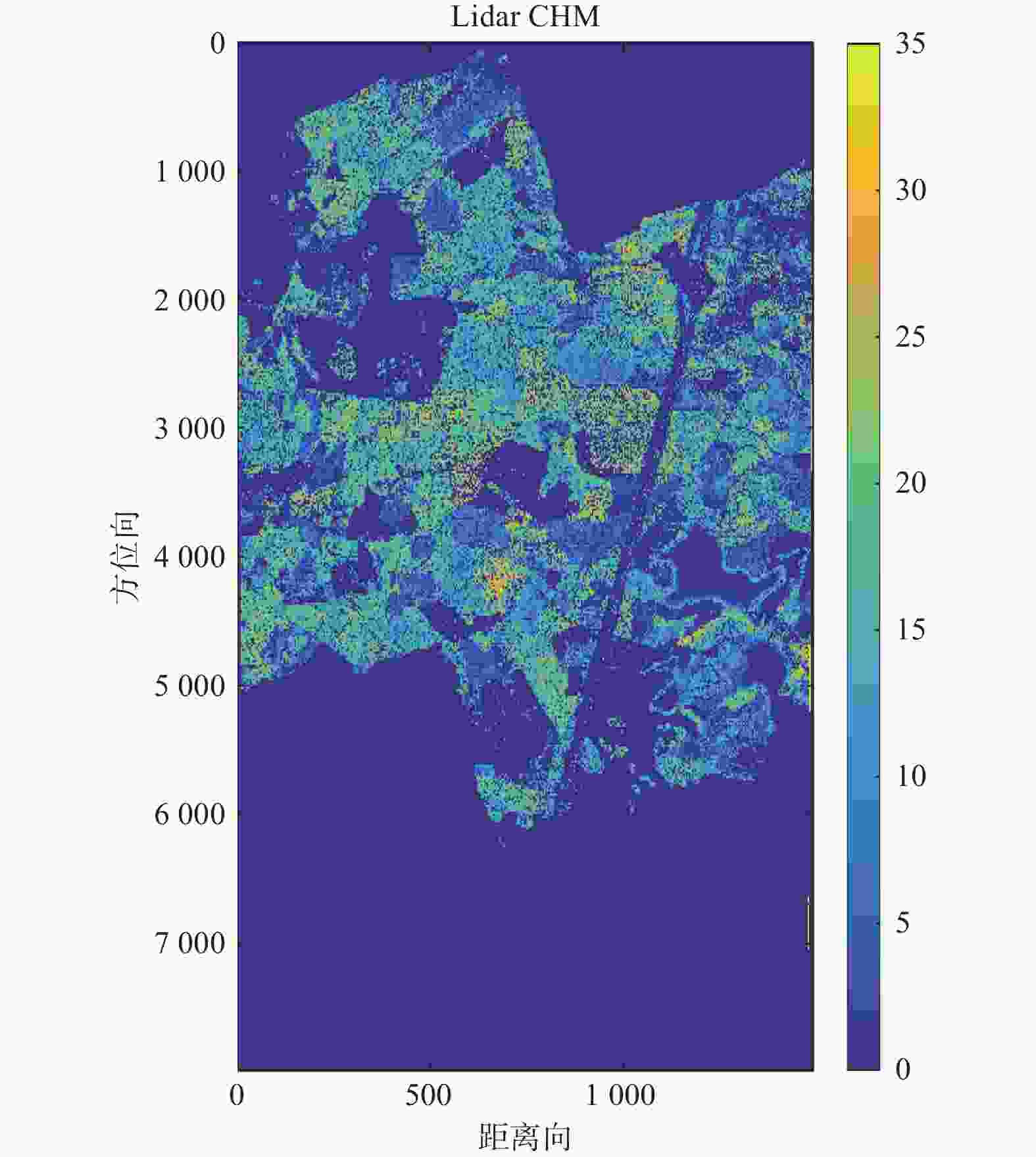
Lidar数据于2010年获取,其中部分区域在2009年已进行测量。Lidar所测的归一化数字表面模型(NDSM),即去除地形信息的DSM,在林区相当于冠层高度模型(CHM)。CHM为树高反演结果提供验证,其空间分辨率为0.5 m×0.5 m,如图2所示。
-
RMoG模型假设植被层由随机分布在粗糙介质层上的垂直物体组成,并且植被冠层和底层都有沿垂直轴的随机运动。在这个假设的基础上,RMoG模型的复相干表述为:
$\gamma = \frac{{\mathop \smallint \nolimits^ \rho \left( Z \right)\exp \left( {j{K_Z}\left( Z \right)} \right)\exp \left( { - \dfrac{1}{2}{{\left( {\dfrac{{4\text{π} }}{\lambda }} \right)}^2}{\sigma ^2}\left( Z \right)} \right)dZ}}{{\mathop \smallint \nolimits \rho \left( Z \right)dZ}}$
(1) 其中σ2(Z)是沿Z轴的一阶近似运动方差,被定义为:
${\sigma ^2}\left( Z \right) = {\sigma _g}^2 + \left( {{\sigma _v}^2 - {\sigma _g}^2} \right)\frac{{Z - {Z_g}}}{{{h_r}}} = {\sigma _g}^2 + \Delta {\sigma ^2}\frac{{Z - {Z_g}}}{{{h_r}}}$
(2) $\varDelta {\sigma ^2} = {\sigma _v}^2 - {\sigma _g}^2$
(3) 其中λ为波长,KZ为垂直波数,一般令
${K_Z} = \dfrac{{4\text{π} \Delta \theta }}{{\lambda \sin \theta }}$ ,hr为参考高度,只是模型的一个常数,不代表需要估计的参数,而且只作为冠层运动的实际参考,因此可以将其固定为任意值;σg和σv分别为地面和冠层运动标准差。ρ(Z)为结构函数,定义了地面和冠层的结构性质、散射分布等,代表了在垂直方向上的平均后向散射密度。与RVoG模型一样,假设冠层散射元素的方向随机,那么ρ(Z)就可写成两部分之和,一部分是与地面有关的狄拉克δ函数,另一部分是与冠层相关的指数函数。将上述式子联合并求解积分,便可得到RMoG模型的最终形式:
$\gamma = {{\rm{e}}^{j{\varphi _g}}}\frac{{\mu {\gamma _{tg}} + {\gamma _{vt}}{{\rm{e}}^{ - j{\varphi _g}}}}}{{1 + \mu }}$
(4) 其中
${\gamma _{tg}} = \exp( - \frac{1}{2}{(\frac{{4\text{π} }}{\lambda })^2}{\varphi _g}^2)$
(5) ${\gamma _{vt}} = {{\rm{e}}^{j{\varphi _g}}}{\gamma _{tg}}\frac{{{P_1}({{\rm{e}}^{\left( {{P_2} + {P_3}} \right)hv}} - 1)}}{{({P_2} + {P_3})\left( {{{\rm{e}}^{{P_1}hv}} - 1} \right)}}$
(6) ${P_1} = \frac{{2\sigma }}{{\cos \theta - {\theta _s}}}$
(7) ${P_2} = {P_1} + j{K_Z}$
(8) ${P_3} = - \frac{{\Delta {\sigma ^2}}}{{2hr}}{\frac{{4\text{π} }}{\lambda }^2}$
(9) 其中hv为植被高度,σ为平均消光系数,θ为雷达入射角,φg为地面相位,μ为地体散射幅度比,θs为沿着距离方向的地面坡度角。
从RMoG模型的公式中可以看出,要求解此方程至少需要5种不同的极化通道;又因为μ随着极化通道的改变而改变,所以极化通道的增加会使未知数的个数增加,当未知数个数大于极化通道个数时,此问题就转化为最优化问题。因此反演时,不可避免的存在长计算时间和对初值敏感的问题。
RMoG模型在RVoG模型的基础上加入了植被高斯运动来减小时间去相关的影响,但由于未知数的增加,使反演问题复杂,反演速度变慢,难以在实际中得到良好的应用。为此,本研究对RMoG模型进行简化;为求解此模型,在借鉴三阶段算法的基础上,将其归结于3步。
-
森林等植被区的时间去相关按照原因可分为3类:一是植被运动造成的时间去相关,如风的影响;二是天气变化引起的介电常数的变化,如降水;三是人为或自然原因引起的场景改变造成的时间去相关。现在的研究大都集中在植被运动引起的时间去相关上[23]。由RMoG模型可知,减弱时间去相关影响的办法为加入植被冠层和底层运动,以此来反映植被运动引起的时间去相关。根据文献[7],为了简化RMoG模型,在数据采集之间的时间间隔较短的情况下,可以将地面运动σg假设为0。当此假设成立时,则
$\Delta {\sigma ^2} = {\sigma _v}^2$ ,γtg=1,于是${\gamma _{vt}}{{\rm{e}}^{ - j{\varphi _g}}}$ 可以简化为:${\gamma _{vt}} = \frac{{{P_1}({{\rm{e}}^{\left( {{P_2} + {P_3}} \right)hv}} - 1)}}{{({P_2} + {P_3})\left( {{{\rm{e}}^{{P_1}hv}} - 1} \right)}}$
(10) 而RVoG模型中体散射公式为:
${\gamma _V} = \frac{{{P_1}{{\rm{e}}^{{P_2}hv}} - 1}}{{{P_2}{{\rm{e}}^{{P_1}hv}} - 1}}$
(11) 与之相比,γvt表达式中增加了植被冠层运动σv;对此,在进行查找表时,可以将消光系数固定,从而建立植被高度hv和冠层运动σv的查找表;而地面相位φg可以从三阶段算法中得到。因此,简化RMoG模型也可以分为3步求解,其步骤如下:
1)在复平面上对多个极化干涉相干系数进行最小二乘直线拟合,该直线与单位圆有两个交点。
2)地面相位与纯体散射去相干的确定。理论上应找到地体散射比μ为0的点对应的相干系数作为纯体散射去相干的估计,但在实际应用中一般选择HV极化通道;由于PD极化相干在体散射去相干上的良好应用[24-25],本研究选择了PDH极化方式作为纯体散射去相干。计算两交点与PDH、PDL的距离,选取距离PDH比距离PDL远的点作为地面相位点。
3)采取合适的消光系数并根据公式10建立查找表,反演最终得到植被高度。
该方法也可以理解为在三阶段算法中加入了植被冠层运动,以此来抵消时间去相关的影响。
-
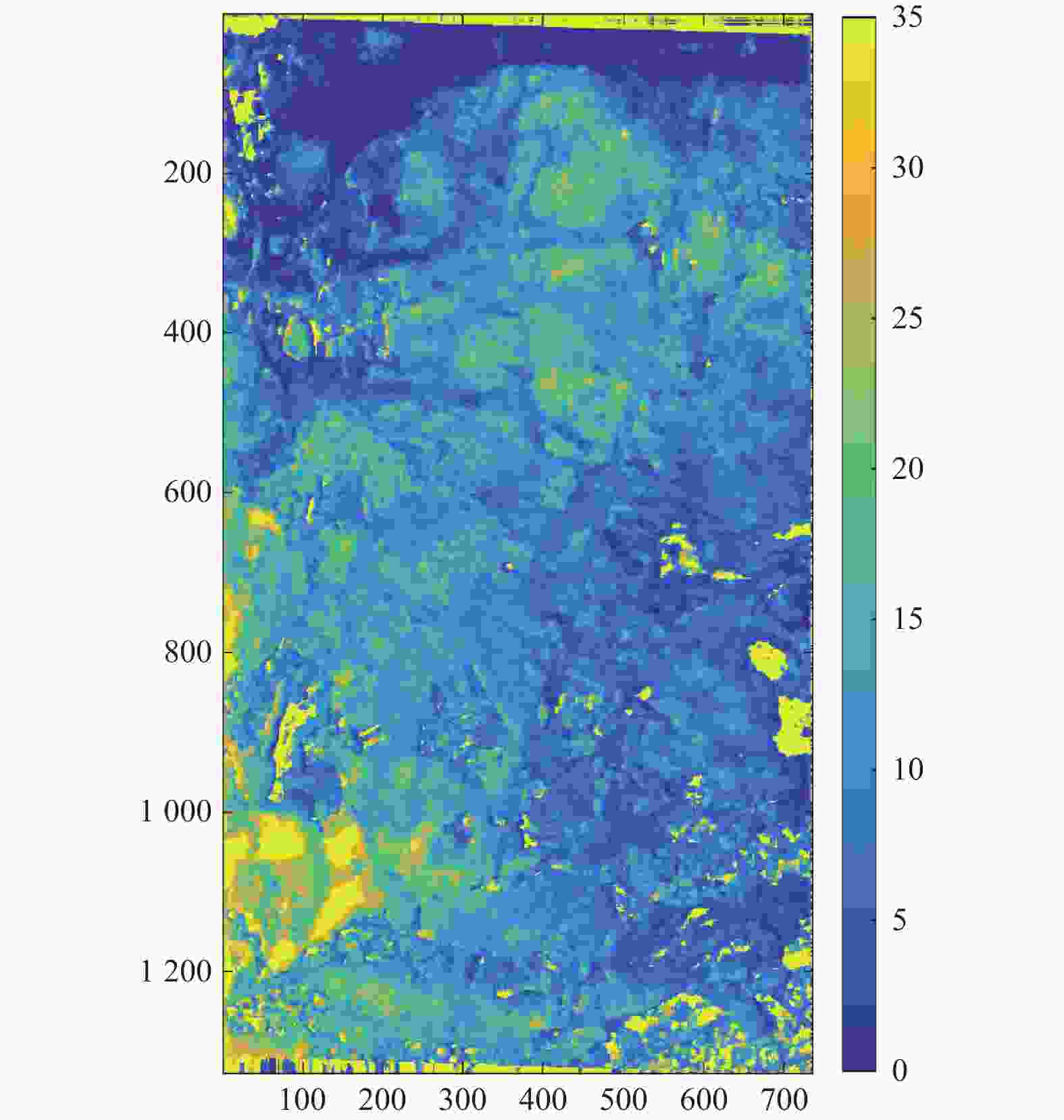
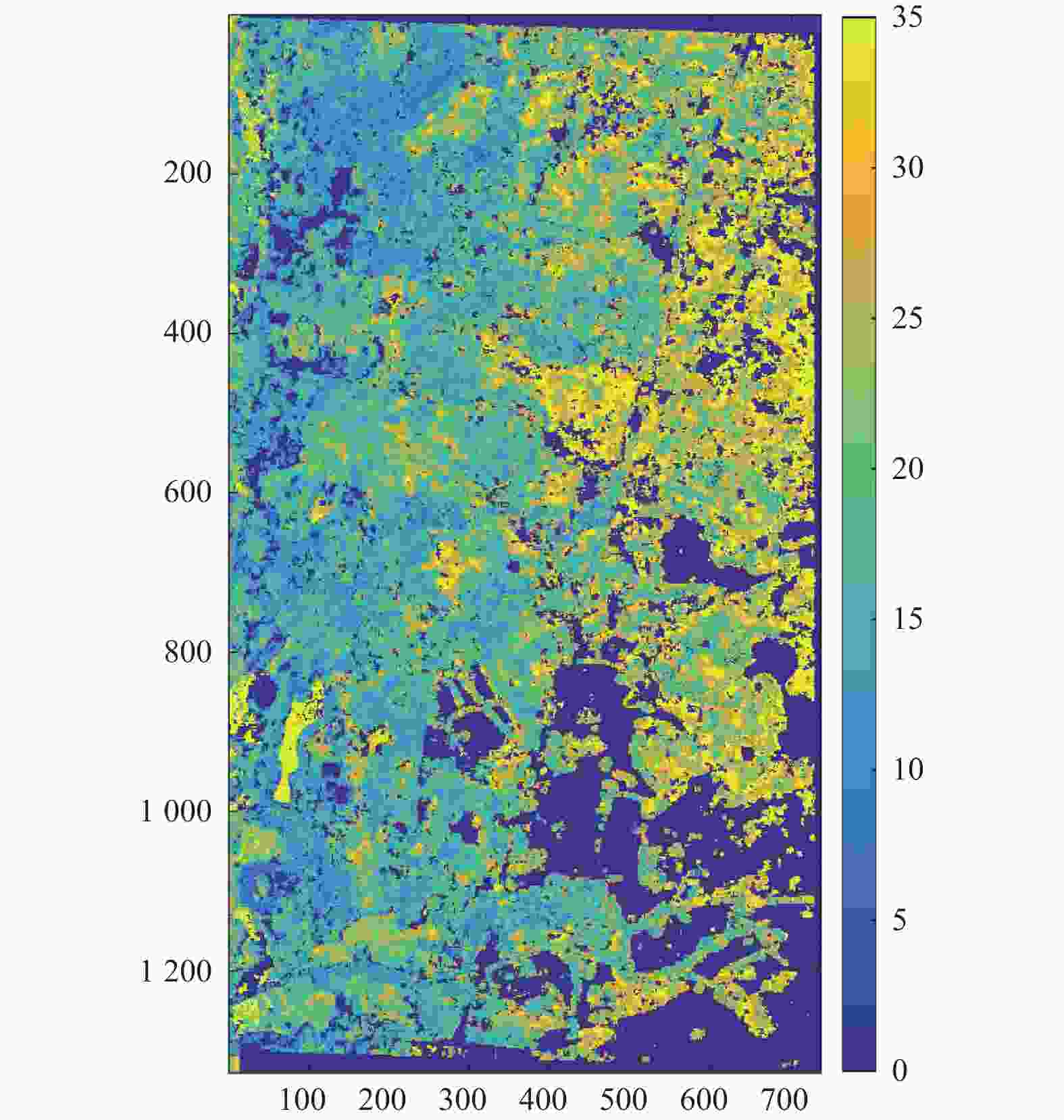
分别用本研究方法和传统三阶段方法对研究区数据进行反演,得到的植被高度图分别如图3和图4所示。RVoG模型中将时间去相关解释为体散射去相关,因此高估了树高;图4与图2对比,可以明显发现图像右边结果高估严重。而本研究方法考虑时间去相关的影响,在模型中加入植被冠层运动,所以对高估问题有显著的改善,并且植被区的结果与Lidar生成的CHM结果较好地吻合。此外,平地效应去除,干涉相干估计等预处理步骤均由PolSARpro软件处理。
-
为定量评价本研究算法的优劣,使用均方根误差(RMSE)和决定系数(R2)为定量评价指标。由于本研究和文献[7]使用的数据在同一地区,所以在比较精度的时候,直接利用了文献[7]中P波段RMoG模型和RMoGL模型的精度,如表1所示。虽然研究区内大部分区域为植被区,但仍有部分湖泊存在;其主要植被区已由Lidar扫描,所以在讨论精度时,只对CHM内像素进行讨论,而对其他区域忽略。
表 1 反演性能比较
Table 1. Inversion performance comparison
森林树高反演方法Inversion method of forest tree height R2 RMSE/m 三阶段算法Three-stage inversion 0.78 8.52 RMoG模型RMoG model 0.47 4.17 RMoGL模型RMoGL model 0.48 2.50 本研究算法Method in this paper 0.53 6.24 从表1可以看出:在均方根误差方面,三阶段算法最差,其次是本研究方法,最好的是RMoGL模型;而在相关性方面,本研究方法和三阶段方法表现较好,最差的为RMoG模型。通过定量的对比可知,本研究方法在精度上有一定的优势;且由于该方法避免了非线性优化过程,可以大大地提高反演速率。
-
在利用PolInSAR数据估计森林参数时,时间去相关是反演模型的关键问题。从RMoG模型出发,继承了其基于高斯运动的时间相干性,并通过忽略地面运动将其简化,称为简化RMoG模型。为避免出现未知数过多现象,采用固定消光系数的方法,并结合查找表使其求解过程更加简单;在有效消除时间去相关影响的前提下,大大缩减反演时间。
Askne等在研究时间去相关时,按照时间基线的长度将时间去相关分为三类:短时间基线内,风速等是产生时间去相关的主要影响因素;中时间基线内,植被区介电常数的改变是产生时间去相关的主要原因;而在长时间基线内,时间去相关可能是植被生长或人为破坏造成[26-28]。本研究的时间去相关主要集中在植被运动也就是风速上,并没有对介电常数或其他进行讨论;换言之,本研究方法只适用于短时间基线或机载SAR数据。
由于消光系数并不是树高反演时的敏感参数,因此本研究采用固定消光系数的方法。但已有研究的实验都是建立树种类型差异不大或树冠形态差异不大的前提下,本研究区满足此条件。然而当多树种或树冠差异较大时,如何固定消光系数,需要更多的实验研究。
-
为更好地从PolInSAR数据估计出森林参数,时间去相关的影响成为不可不解决的问题。在时间去相关方面,RMoG模型和RMoGL模型都有着较好的反演精度,但由于其难以求解、耗时较长的原因并不能很好地应用。本研究将RMoG模型简化,忽略地面运动,在保证反演精度的同时,提高了反演效率。通过BioSAR2007数据的试验,可以得到以下结论:与未加入时间去相关的RVoG模型对比,简化RMoG模型只加入植被冠层运动抵消时间去相关影响的方法行之有效,并且反演结果明显改善,得到的高度图更接近Lidar生成的CHM,从中可以看出考虑时间去相关的重要性和必要性;在精度对比方面,与三阶段算法相比,本研究方法的精度有所提升,均方根误差由8.52降到6.24;与RMoG模型和RMoGL模型相比,本研究方法虽然略有不足,但由于忽略植被地面运动,很好地改善了RMoG模型和RMoGL模型反演困难、耗时过长的缺点。本研究方法可以有效消除时间去相关的影响,且使反演过程更加高效。
基于时间去相关的三阶段森林高度估计方法
Three-stage Tree Height Inversion Algorithm with Compensation for Temporal Decorrelation
-
摘要:
目的 在利用极化SAR数据反演树高时,时间去相关因子是影响反演精度的主要因素;目前,地面随机运动模型(RMoG)是该领域最有效的模型之一,但地面随机运动模型有着反演困难、耗时过长的缺点。为了改善这个问题,提出了简化RMoG模型。 方法 首先忽略地面运动,只保留植被冠层运动,重新改写植被体散射公式;然后对多个相干系数直线拟合出地面相位;再次通过PD极化相干最优方法来估计纯体散射去相干值;最后利用改写后的植被体散射公式建立查找表,在固定消光系数的基础上通过查找表反演得到植被高度。为了验证本研究方法的有效性,以瑞典南部的Remingstorp地区为研究区,以BioSAR2007项目的遥感数据进行试验,并以决定系数(R2)和均方根误差(RMSE)对4种模型的反演结果进行比较评价。 结果 表明:本研究方法可以很好地改善三阶段算法的高估问题。在精度比较方面:三阶段算法的R2为0.78,RMSE为8.52;RMoG模型的R2为0.47,RMSE为4.17;RMoGL模型的R2为0.48,RMSE为2.50;本方法的R2为0.53,RMSE为6.24。对比三阶段算法,本研究方法在精度上有明显的优势;对比RMoG模型和RMoGL模型,本方法可有效地减少反演时间。 结论 通过添加植被冠层运动消除时间去相关的影响行之有效。与三阶段算法、RMoG模型和RMoGL模型对比,本方法具有精度高、耗时少的优点。 Abstract:Objective When polarimetric SAR data are used to invert tree height, time decorrelation factor is the main factor affecting inversion accuracy. Random-Motion-over-Ground (RMoG) model is one of the most effective models, but it has the disadvantages of difficult inversion and long time-consuming. Here, a simplified RMoG model is proposed. Method In this study, the ground motion was neglected, the vegetation canopy motion was retained, and the vegetation volume scattering formula was rewritten. Then, the ground phase was judged by linear fitting of multiple coherence coefficients, and the decoherence value of pure volume scattering was estimated by PD polarization coherence optimization method. Finally, the rewritten vegetation volume scattering formula was used to establish a survey. Based on the fixed extinction coefficient, the height of vegetation can be retrieved by looking-up table. To verify the validity of this method, the remote sensing data of BioSAR 2007 project were tested in Remingstorp, southern Sweden. The inversion results of the four models were compared and evaluated with the determination coefficient (R2) and the root mean square error (RMSE). Result This method can improve the overestimation problem of three-stage algorithm. In terms of accuracy comparison, the R2 of three-stage algorithm is 0.78 and RMSE is 8.52; the R2 of RMoG model is 0.47 and RMSE is 4.17; the R2 of RMoGL model is 0.48 and RMSE is 2.50; the R2 of this method is 0.53 and RMSE is 6.24. It is showed that this method is better in accuracy compared with three-stage algorithm, and can effectively reduce the inversion time compared with RMoG model and RMoGL model. Conclusion It is effective to eliminate time-related effects by adding vegetation canopy movement. Compared with three-stage algorithm, RMoG model and RMoGL model, the simplified RMoG model has the advantages of high accuracy and less time-consuming. -
表 1 反演性能比较
Table 1. Inversion performance comparison
森林树高反演方法Inversion method of forest tree height R2 RMSE/m 三阶段算法Three-stage inversion 0.78 8.52 RMoG模型RMoG model 0.47 4.17 RMoGL模型RMoGL model 0.48 2.50 本研究算法Method in this paper 0.53 6.24 -
[1] Fang, J. Changes in forest biomass carbon storage in China between 1949 and 1998[J]. Science, 2001, 292(5525): 2320-2322. doi: 10.1126/science.1058629 [2] Houghton R A. Aboveground forest biomass and the global carbon balance[J]. Global Change Biology, 2005, 11(6): 945-958. doi: 10.1111/j.1365-2486.2005.00955.x [3] Mette T, Papathanassiou K, Hajnsek I, et al. Applying a common allometric equation to convert forest height from Pol-InSAR data to forest biomass[C]// IEEE International Geoscience & Remote Sensing Symposium. IEEE, 2004. [4] Wenxue F, Huadong G, Xinwu L, et al. Extended three-stage polarimetric SAR interferometry algorithm by Dual-Polarization Data[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(5): 2792-2802. [5] 吴一戎, 洪 文, 王彦平. 极化干涉SAR的研究现状与启示[J]. 电子与信息学报, 2007, 29(5):1258-1262. [6] 李廷伟, 梁甸农, 朱炬波. 极化干涉SAR森林高度反演综述[J]. 遥感信息, 2009(3):86-92. [7] Nafiseh G, Valentyn T, Alfred S. A modified model for estimating tree height from PolInSAR with compensation for temporal decorrelation[J]. International Journal of Applied Earth Observation and Geoinformation, 2018, 73: 313-322. doi: 10.1016/j.jag.2018.06.022 [8] Papathanassiou K P, Cloude S R. Single-baseline polarimetric SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2352-2363. doi: 10.1109/36.964971 [9] Cloude S R, Papathanassiou K P. Three-stage inversion process for polarimetric SAR interferometry[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(3): 125-134. doi: 10.1049/ip-rsn:20030449 [10] 许丽颖, 李世强, 邓云凯, 等. 基于极化干涉SAR反演植被高度的改进三阶段算法[J]. 雷达学报, 2014, 3(1):28-34. [11] 谈璐璐, 陈 兵, 杨汝良. 利用POLInSAR数据反演植被高度的改进三阶段算法[J]. 系统仿真学报, 2010, 22(4):996-999. [12] Zhou Y S, Hong W, Cao F, et al. Analysis of temporal decorrelation in dual-baseline polinsar vegetation parameter estimation[C]//. IEEE International Geoscience and Remote Sensing Symposium, 2008., 473-476. [13] Mette T, Kugler F, Papathanassiou K, et al. Forest and the random volume over ground - nature and effect of 3 possible error types[C]// European Conference on Synthetic Aperture Radar (EUSAR). DLR, 2006. [14] Lee S K, Kugler F, Hajnsek I, et al. The impact of temporal decorrelation over forest terrain in polarimetric SAR interferometry[C]// Proceedings of the Fourth International Workshop on Science & Applications of SarPolarimetry&Polarimetric Interferometry Poiinsar, 2009, 668. [15] Lee S K, Kugler F, Papathanassiou K, et al. Quantifying temporal decorrelation over boreal forest at L- and P-band[C]// European Conference on Synthetic Aperture Radar. VDE, 2011. [16] Lee S K, Kugler F, Papathanassiou K, et al. Quantification and compensation of temporal decorrelation effects in polarimetric SAR interferometry[C]// IEEE International Geoscience and Remote Sensing Symposium (IGARSS). IEEE, 2012. [17] Papathanassiou K P, Cloude S R. The effect of temporal decorrelation on the inversion of forest parameters from Pol-InSARdata[J]. IEEE International Geoscience and Remote Sensing Symposium, 2003, 3: 1429-1431. [18] Zhou Y S, Hong W, Cao F, et al. Analysis of temporal decorrelation in dual-baseline polinsar vegetation parameter estimation[C]// Geoscience and Remote Sensing Symposium, 2008. IGARSS. IEEE, 2008. [19] Lavalle M, Simard M, Pottier E, et al. Polinsar forestry applications improved by modeling height-dependent temporal decorrelation[C]// IEEE International Geoscience & Remote Sensing Symposium. IEEE, 2010. [20] Lavalle M, Simard M, Solimini D, et al. Height-dependent temporal decorrelation for POLINSAR and TOMOSAR forestry applications[C]// European Conference on Synthetic Aperture Radar. VDE, 2011. [21] LavalleM, Simard M, Hensley S. A temporal decorrelation model for polarimetric radar interferometers[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(7): 2880-2888. [22] Lavalle M, Hensley S. Extraction of structural and dynamic properties of forests from polarimetric-interferometric SAR Data affected by temporal decorrelation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(9): 4752-4767. doi: 10.1109/TGRS.2015.2409066 [23] 李 震, 郭 明, 汪仲琼, 等. 星载重轨极化干涉SAR反演森林植被高度[J]. 中国科学: 地球科学, 2014(4):680-692. [24] 伍雅晴, 朱建军, 付海强, 等. 引入PD极化相干最优的三阶段植被高度反演算法[J]. 测绘通报, 2016(5):32-35, 76. [25] 罗环敏, 陈尔学, 程 建, 等. 极化干涉SAR森林高度反演方法研究[J]. 遥感学报, 2010, 14(4):806-821. [26] Askne J I H, Dammert P B G, Ulander L M H, et al. C-band repeat-pass interferometric SAR observations of the forest[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 0-35. [27] Askne J, Santoro M. Multitemporal repeat pass SAR interferometry of boreal forests[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(6): 1219-1228. doi: 10.1109/TGRS.2005.846878 [28] Askne J, Santoro M. Selection of forest stands for stem volume retrieval from stable ERS tandem inSAR observations[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(1): 46-50. doi: 10.1109/LGRS.2006.883525 -



 下载:
下载: