-
林木的枯损是森林生长过程中十分重要的组成部分,但又是一个知之甚少的森林动态过程[1-3]。对林木枯损进行准确的预测是森林生长收获预估系统中十分重要的工作[4]。最早预测林木的枯损是通过建立枯损与协变量的回归方程来预测枯损概率,之后一些学者也采用此方法估计林木的枯损概率[5]。由于林木的枯损是典型的二分量数据,只包括是否枯损两种结局,因此此类方法的模拟效果并不理想。Logistic回归分析方法对于二分量数据具有先天的优势,Hamilton[6]和Monserud[7]引入了此方法来模拟林木的枯损,目前已被广泛应用[8-10]。但是上述方法在模拟林木枯损时,缺乏把树木枯损的时间特性、假设检验、删失数据的观测和协变量的影响同时考虑[11]。即不能够给出树木具体的生存或死亡时间,也不能预测未来林木的发展趋势[12]。林木枯损数据的这些特性使得利用传统的统计方法处理具有困难,但是忽略它们将降低模型估计的准确性[13]。
生存分析方法既考虑观测对象的事件结局“生存”或“死亡”,又能够考虑观测对象的生存时间长短,可为构建新的林木枯损模型提供支撑。是唯一考虑删失数据,并且包括时间协变量,另外能够处理非正态分布数据的一类方法[11]。Waters[14]第一次建议利用生存分析方法来描述林木的枯损问题,但仅限于同龄林分。随着统计学和计算机技术的快速发展,生存分析方法逐渐地被用到分析和构建林木的枯损模型中。例如,Woodall等[11]采用生存分析方法中的生命表法(lifetime table),Fan等[15]利用Kaplan-Meier方法,von Gadow等[16]利用服从Weibull时间分布的参数方法,Uzoh等[17]利用Cox比例风险函数模型来分析上层林木的枯损。这些学者把林木的枯损和生存时间结合起来,取得了很好的模拟和预测结果。
在构建枯损模型时,很多数据都是基于永久性固定样地的多次定期观测,每个林分包括多个样地,每个样地包括多株枯损树木,这些数据存在着多层嵌套结构。另外林木在生长过程中,受竞争及干扰等诸多因素的影响,导致了林木枯损具有很高的时空变化性[18]。在利用生存分析方法构建枯损模型时,忽略这些问题将会造成大的误差。生存分析方法结合混合效应模型方法是一种新的思路,可解决上述诸多问题,并且能够提高模型的模拟精度。目前把两者结合起来构建林木枯损的模型还未见诸于文献。
本研究以1986年在吉林省汪清林业局金沟岭林场设置的20块落叶松云冷杉样地数据为例,利用生存分析方法中的半参数Cox比例风险函数模型来进行林木的枯损及生存模拟,并采用逐步回归方法把对枯损具有重要影响的林分因子和立地因子作为协变量加入到林木枯损模型中去,选择Schoenfeld残差方法(Schoenfeld residuals)分析模型的适应性,在适应的模型基础上考虑样地的随机效应。并对传统方法与考虑样地随机效应的模拟结果进行比较分析。最后按对枯损有影响的协变量的不同情况,预测不同时间内林木的生存率。
-
本研究选择了位于吉林省汪清林业局金沟岭林场境内的1986年设置的20块落叶松云冷杉混交林为研究对象,优势树种主要包括长白落叶松(Larix olgensis Henry)、云杉(Picea jazoensis Nakai)和冷杉(Abies nephrolepis (Trautv.) Maxim)等,其他伴生树种包括红松(Pinus koraiensis Siebold et Zuccarini)、白桦(Betula platyphylla Suk.)、枫桦(Betula costata Trautv.)和水曲柳(Fraxinus mandshurica Rupr.)等。所有样地从1987年开始,分别在1988、1990、1992、1994、1997、1999、2002、2004、2006、2008、2009和2012年进行了调查。调查的样地因子包括坡度、海拔、坡向、土壤类型、土层厚度等内容。调查因子包括每木检尺(胸径>5 cm)、林木枯损情况、枯损时间、枯损原因、林下更新及林下植被等。其中2块样地在1987年和1993年进行了2次间伐,其余18块只在1987年进行了间伐,因此只选择了18块样地,共3 477株树木进行分析。外业调查结束后,对林分平均直径、公顷株数、公顷断面积、大于对象木断面积(BAL)、公顷蓄积量和直径比等指标进行了计算。其中大于对象木断面积的定义为具体一个样地内,任意一株树木,胸径大于它的所有树木的断面积之和。从1987—2012年整个观测期间,共有1 352株树木发生枯损。1987年伐后调查的样地因子概况见表1。
表 1 样地1987年基本情况
Table 1. The characteristics of experimental stands established plot
样地号
Plot number面积
Area/hm2海拔
Elavation/m坡向
Aspect坡度
Slope平均胸径
The mean diameter/cm公顷株数
The stem number/(N·hm−2)公顷断面积
Basal area per hectare/(m2·hm−2)301 0.077 5 760 东北 10 14.93 955 16.83 302 0.077 5 760 东北 10 14.71 1 572 26.69 303 0.13 760 东北 10 14.26 1 098 17.64 304 0.097 5 760 东北 10 15.88 883 17.56 305 0.2 780 西 18 15.07 1 158 20.64 306 0.2 780 东北 7 13.66 2 008 29.42 307 0.2 780 西 18 15.02 1 153 20.50 308 0.2 780 东北 10 15.82 846 16.39 309 0.25 660 西北 6 15.61 1 189 22.86 310 0.25 670 西北 10 16.18 860 17.74 311 0.25 670 西北 6 17.20 833 19.39 312 0.25 680 西北 10 15.49 914 17.30 315 0.112 5 660 北 7 13.58 1 694 24.44 316 0.1 645 北 7 14.87 1 127 19.66 317 0.1 615 东北 7 13.51 1 286 18.65 318 0.112 5 610 东北 7 14.39 919 15.03 319 0.1 605 东北 9 15.17 820 14.84 320 0.1 600 东北 9 13.65 1 670 24.41 -
生存分析方法的基本概念可参考文献Allison[19]和Lawless[20],常用概率密度函数(
$f(t)$ )、生存函数($S(t)$ )以及风险函数($h(t)$ )等3个函数来描述生存过程。这3种函数在数学上是等价的。如果给定其中一种函数,另两种函数即可推导得出。在构建林木的枯损模型时,生存时间虽为定量指标,但往往不服从任何规则分布,要在这种情况下确定林木的枯损时间和各风险因素之间的定量关系,就不能够采用参数方法来达到目的。Cox比例风险函数模型可直接建立终点事件的发生风险与这些影响因素之间的函数关系[21]。本研究采用Cox比例风险函数模型和样地水平的随机效应,对应的风险函数可以表示为式(1):$h(t|X) = {h_0}(t)\exp (\beta {x^T} + {b_i})$
(1) ${h_0}(t)$ 是仅与时间有关的风险函数,其分布没有明确的假设,是模型的非参数部分,$\exp (\beta {x^T})$ 是在${h_0}(t)$ 效应基础上产生作用的,估计值不受时间影响,是模型的参数部分。${b_i}$ 为样地($i = 1,2, \cdot \cdot \cdot, 18$ )间截距的随机效应值,服从均值为0,方差为${\sigma ^2}$ 的正态分布。在进行生存分析时,影响林木枯损的因子是作为协变量加入到模型中去。影响林木枯损的因子很多,本研究只考虑立地因子和调查初始林分因子对林木枯损的影响。林分因子主要包括树种本身的特性、林分密度、林分结构及林木间的竞争等[22-24]。本研究主要选择的林分因子包括单木初始胸径、单木初始胸径与林分平均胸径的比值、大于对象木断面积、初始林分公顷株数、初始林分公顷断面积、初始林分公顷蓄积、初始林分平均胸径等指标因子。立地因子影响森林环境中光照、温度、水分、土壤等的分布,进而影响林木的枯损状况[25]。本研究主要选择坡度、坡向及海拔等因子对林木枯损的影响[26]。
-
在选择Cox半参数方法进行林木枯损及生存模拟时,首先要判断实验数据是否满足Cox比例风险函数模型的假设。拟合优度检验方法是十分普遍的方法[27],其主要思想是首先计算待检验变量的Schoenfeld的残差,然后对非删失数据的生存时间排秩,最后利用残差图来检验Schoenfeld残差与时间秩的相关性。如果两者存在关联性则认为该数据不满足Cox比例风险假设。具体的Schoenfeld残差公式见式(2):
$ {\rm{Schoenfeld}}{\text{残差}}={x_{ik}} - \sum\limits_{m \in R({t_i})} {{x_{mk}}{p_m}} $
(2) 其中,
${x_{ik}}$ 为在${t_i}$ 时刻发生枯损的林木的第$k$ 个协变量的实际取值,${x_{mk}}$ 为${t_i}$ 时刻尚在风险集里的林木$m$ 的第$k$ 个协变量取值,${p_m}$ 为风险集中林木$m$ 在${t_i}$ 时刻发生枯损的概率。在采用Schoenfeld残差图判断是否可以用Cox比例风险函数后,本研究采用Wald指标来评价模型本身的模拟效果。在比较不同模型的拟合效果优劣时,采用AIC信息准则(Akaike information criterion,AIC)、BIC信息准则(Bayesian Information Criterion,BIC)和-2*对数似然值(-2*Loglikelihood,-2LogL)这3个值。这3个值越小,说明模型的模拟效果越好[28-30]。LRT卡方检验被用来比较模型之间的差异显著程度[31]。
-
把所有备选的林分因子和立地因子作为协变量加入到Cox比例风险函数模型中去,利用SAS9.4软件进行模拟。考虑各因子之间存在的多重共线性(VIF<5)和显著影响(
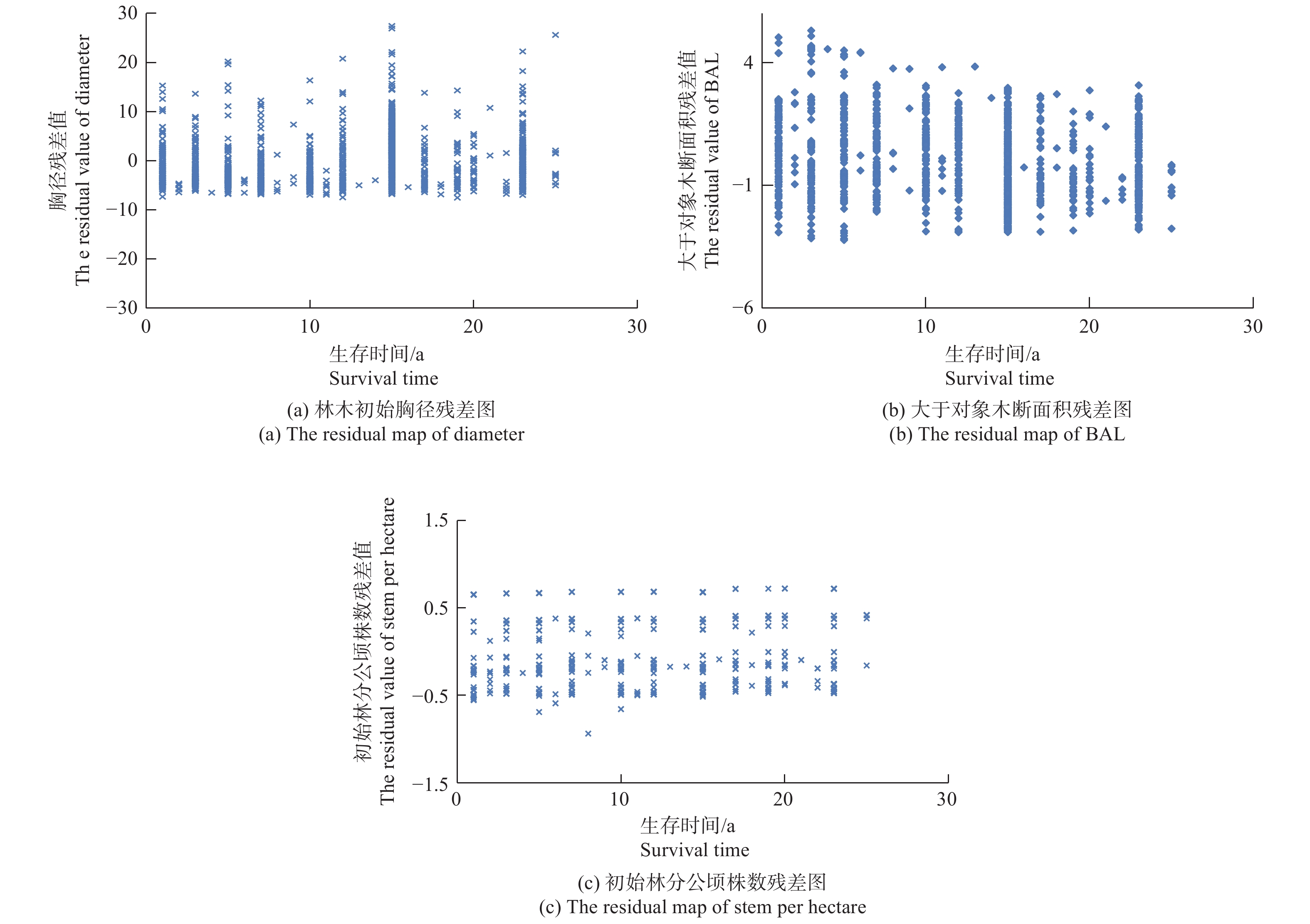
$\alpha < 0.05$ )情况下,结果最后只有单木初始胸径、大于对象木断面积和初始林分公顷株数等林分因子对林木的枯损具有重要的影响。而立地因子的3个具体因子对林木的枯损均没有显著影响,具体模拟结果见表2的模型1(M1)。利用Schoenfeld残差分布图来判断实验数据及协变量是否满足Cox比例风险函数模型的条件假设,结果见图1。从图1的3个残差图可以看出,单木初始胸径与观测时间不呈线性关系、大于对象木断面积、初始林分公顷株数与观测时间不呈线性关系,说明本次研究采用的数据完全符合Cox比例风险函数的条件假设,可以选择Cox比例风险函数来构建林木的枯损模型。Wald指标表明,在考虑了3个协变量后,3个模型的模拟效果差异均极度显著(p<0.000 1),能够满足模型的精度要求。进一步在Cox模型的基础上,考虑样地的随机效应,本研究只考虑了样地的截距效应,结果为模型的AIC、BIC和-2LogL3个值均比不考虑随机效应值小,LRT卡方检验表明,差异达显著水平(见表2的模型2)。由于考虑了样地的随机效应后,大于对象木断面积和初始林分公顷株数两个协变量差异不显著(p>0.05),因此去掉了这两个协变量,然后重新模拟,结果见表2的模型3(M3)。最后结果表明,当考虑样地水平的随机效应后,去掉大于对象木断面积和初始林分公顷株数两个协变量后,模型精度并没有降低,两者之间没有显著差异(LRT=4.2,$p > 0.05$ )。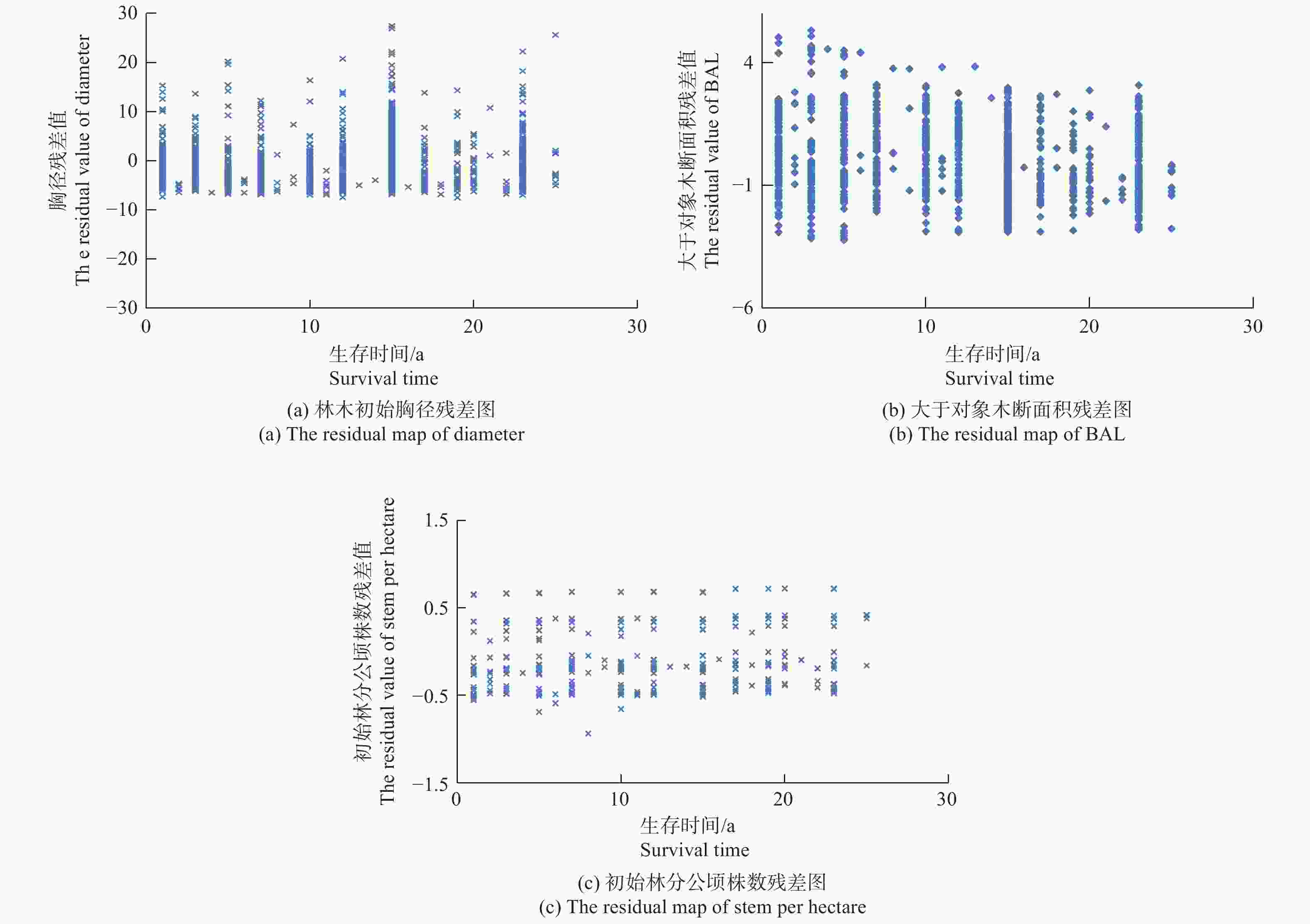
图 1 各协变量与观测时间的残差分布
Figure 1. The residual figure between estimate and measure result of covariate variable
表 2 Cox比例风险函数模型模拟结果
Table 2. The result of Cox proportional hazard model
协变量
Covariatevariable模型1(M1)
Model 1模型2(M2)
Model 2模型3(M3)
Model 3估计值(标准差)
Estimate result(Standard error)P值
P value估计值(标准差)
Estimate result(Standard error)P值
P value估计值(标准差)
Estimate result(Standard error)P值
P value单木初始胸径
Initial DBH/d−0.052 7(0.007 6) <0.000 1 −0.077 8(0.012 4) <0.000 1 −0.089 5(0.006 5) <0.000 1 大于对象木断面积(BAL)
Basal area of the trees larger
than the subject tree/(m2·hm−2)0.104 7(0.021 1) <0.000 1 0.056 4(0.048 5) 0.244 7 初始林分公顷株数
Initial stem number/(N·hm−2)0.656 5(0.066 4) <0.000 1 0.535 8(0.311 2) 0.085 2 Wald指标
Wald value304.078 9 <0.000 1 528.049 0 <0.000 1 523.407 5 <0.000 1 AIC 21 164.6 20 944.6 20 948.8 BIC 21 180.3 20 960.3 20 964.5 −2LogL 21 158.6 20 938.6 20 942.8 LRT M2/M1LRT=220($p < 0.001$) M3/M2LRT=4.2($p > 0.05$) 从表2的结果可以看出,单木的初始胸径与林木枯损的风险率呈反比,与生存率呈正比,初始胸径大的林木,枯损的风险低于胸径小的林木,进而生存率高于胸径小的林木。这与利用logistic方法模拟枯损的结论基本一致[32]。
-
在实际林分中,胸径小的树木在林分中处于竞争的劣势,对水、肥、气、热等资源的竞争处于不利地位。而胸径大的树木处于竞争的优势,更加有利于争夺林分中的营养。因此,胸径小的树木更容易发生枯损。为了直观的表述初始胸径与林木枯损的关系,进一步选择初始胸径为10、15和20 cm的3株树木,在初始林分密度均为2 000株·hm−2的林分内,在不考虑其他因子影响的前提下,利用Cox比例风险函数模型来估计其生存率,并绘制生存曲线,见图2。从图中可以看出,随着时间的推移,胸径大的树木其生存率始终高于胸径小的树木,这和上述模拟的结果一致。在同一林分内,一般初始胸径小的林木其大于对象木断面积值就大,因此与初始胸径相反,大于对象木断面积与林木枯损的风险率呈正比,与生存率呈反比。
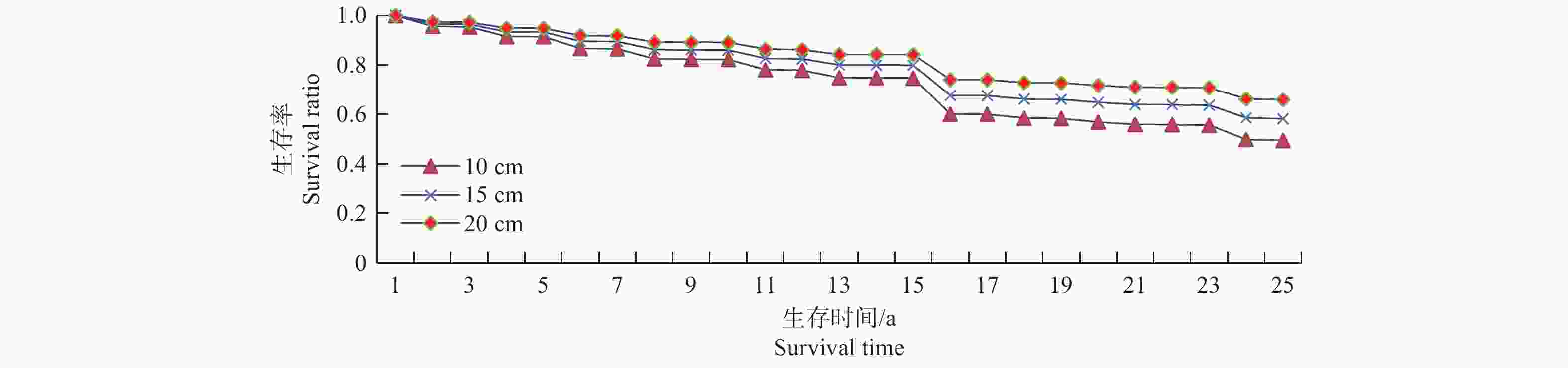
图 2 10、15和20 cm初始胸径树木生存率(
$S(t)$ )趋势Figure 2. Thesurvival curve of tree of initial diameter with 10, 15 and 20 cm
林分公顷株数是一个重要的影响因子,属于林分层次,反映了林分的密度情况。本研究中初始林分公顷株数与林木枯损的风险率呈正比,与生存率呈反比。这说明,林分密度越大,林木枯损的风险越大,生存率越低,越容易枯损[8,26]。为了更直观的表示林分公顷株数对枯损的影响,进一步选择胸径为15 cm的树木在初始林分密度为1 000,1 500和2 000株·hm−2的3个林分情况下,在不考虑其他因子影响的前提下,利用Cox比例风险函数模型来计算其生存率,并绘制生存曲线,见图3。
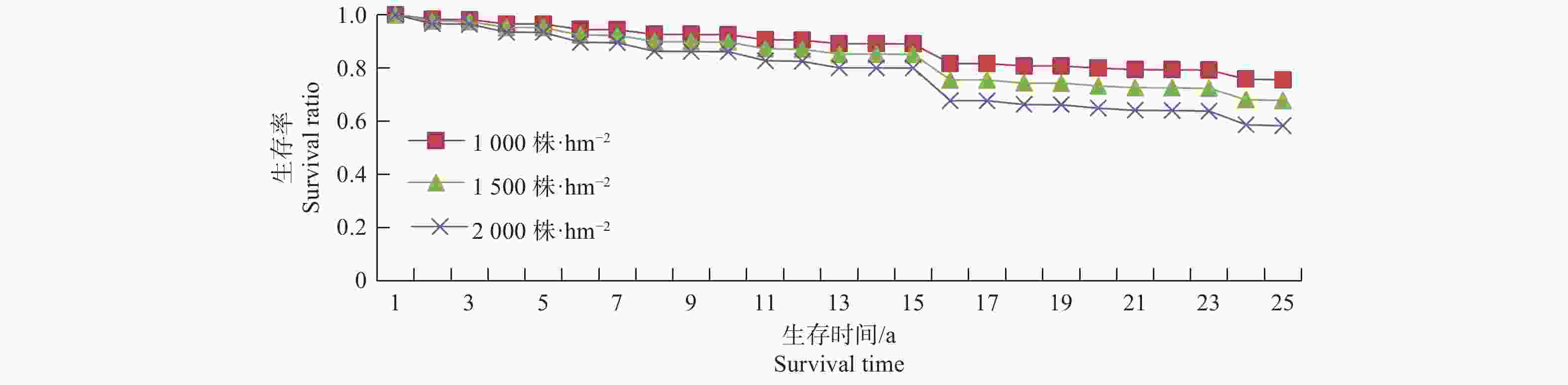
图 3 初始林分密度为1 000,1 500和2 000株·hm−2的林木生存率(
$S(t)$ )趋势Figure 3. The survival curve of tree with initial stand density of 1 000, 1 500 and 2 000 trees·hm−2
从图3可以看出,胸径为15 cm的树木,在整个测量区间,随着时间的推移,初始林分密度大的林分,林木的枯损概率逐渐增大并且生存率较初始密度小的林分快速降低。这充分说明,同一株林木,初值密度越大,对资源的竞争越激烈,与初始林分密度小的林分相比,林木的生存率越低。
立地因子对林木的枯损没有任何影响,造成这一原因可能是选择的20块落叶松云冷杉样地分布在一个林场内,坡度、坡向和海拔本身的差别小,难以体现在对枯损的影响上。
从图2和图3可以看出,林木在观测15 a至16 a之间生存率有一个明显的下降。从数据本身来看,从1986—2012年整个观测期内共枯损1 352株树木,而在1999—2002年观测期间就枯损了405株,差不多占整个枯损量的三分之一。造成这一期间大量枯损的原因可能是极端气候引起的(干旱,霜冻),由于本研究没有考虑气象因子对枯损的影响,因此无法获得确切的原因,今后需要进一步考虑。
Cox比例风险函数在考虑了样地的随机截距效应后,模型的模拟精度显著提高,并且差异达显著程度。但是初始林分密度和大于对象木断面积的影响差异并不显著,在去掉这两个协变量重新模拟后发现模型的模拟效果并没有降低。因此,初始胸径是最重要的影响林木本身枯损的指标[33-34]。
-
本研究利用Cox比例风险函数描述落叶松云冷杉林木的枯损情况,并考虑了样地的随机效应,取得了很好的效果。林木初始胸径、大于对象木断面积及初始林分公顷株数对林木的枯损具有重要的影响。在考虑样地的随机效应后,模型的模拟效果显著提高,说明样地的枯损存在着明显的高可变性和随机性。在实际中,林木初始胸径是不容易控制的指标,但是初始林分密度可通过科学的采伐来调节。如果想降低林木的枯损率,可适当降低林分的密度,进而能够促进林木本身胸径的生长。本研究基于生存分析方法为林木的枯损研究提供了可借鉴的新思路。Cox比例风险函数模型的使用,使得森林经营者在制定森林采伐方案及采伐时间上提供了很好的科学依据。
基于Cox比例风险函数及混合效应的落叶松云冷杉混交林林木枯损模型研究
Mortality Model of Larix olgensis-Abies nephrolepis-Picea jazoensis Mixed Stands Based on Cox Proportional Hazard Function and Mixed Effect Model
-
摘要:
目的 将生存分析方法和混合效应模型方法相结合,构建林木枯损模型,提高模型的模拟精度。 方法 以吉林省汪清林业局20块落叶松云冷杉林样地数据为材料,基于生存分析方法中的Cox比例风险函数模型方法,把林分因子和立地因子作为协变量加入到模型中去,构建林木的枯损及生存模型,并在此基础上考虑样地水平的随机效应,最后与不考虑样地水平随机效应的模拟效果进行比较分析。 结果 表明,Cox比例风险函数模型在描述林木枯损时,具有很好的适应性。单木初始胸径与林木的风险函数呈反比,与生存率呈正比;大于对象木断面积与风险函数呈正比,与生存率呈反比;初始林分公顷株数与风险函数呈正比,与生存率呈反比;立地因子对林木的枯损及生存没有显著影响。与固定效应模型相比,Cox比例风险函数模型在考虑了样地水平的随机效应后,模型的模拟精度获得明显的提高,并且达到极显著程度。由于大于对象木断面积和初始林分公顷株数两个变量在考虑了样地水平的随机效应后影响不显著,最后只考虑了单木初始胸径一个变量对枯损的影响,与不考虑随机效应相比,差异也达到显著水平。 结论 林木本身的大小对自身的枯损具有明显的影响,胸径小的林木较胸径大的林木更易枯损。在森林经营中,Cox比例风险函数模型的使用,可为森林经营者在确定合理的经营密度上提供很好的科学依据。 Abstract:Objective The survival analysis method and mixed effect model are combined to construct tree mortality model and improve the simulation precision of the model. Method Taking 20 plots of Larix olgensis-Abies nephrolepis-Picea jazoensis mixed stand in Wangqing Forestry Bureau of Jilin Province as examples, the tree mortality and survival model were constructed based on Cox proportional hazard function of survival analysis method, and the stand factor and site factor was added into the model as covariates. The plot’s random effect was considered and compared with the simulation effect of the traditional model. Result It showed that the Cox proportional hazard function model had fitting goodness in describing tree mortality. The initial DBH of tree was negatively correlated with the hazard function of the tree, and positively correlated with survival rate. The BAL was positively correlated with the hazard function of the tree, and negatively correlated with survival rate. The initial stand density per hectare was positively correlated with the hazard function of the tree, and negatively correlated with survival rate. Compared with the fixed effect model, the accuracy of Cox proportional hazard function model was greatly improved after considering plot’s random effect. Because the BAL and initial stand density per hectare showed no significant effect after considering the plot’srandom effect, only the initial DBH was considered, and the difference also reached a significant level. Conclusion In forest management, the Cox proportional hazard function model provides a good basis for determining the reasonable management density for forest operators. -
Key words:
- survival analysis
- / mixed effects model
- / mortality
- / Cox proportional hazard function
- / hazard ratio
-
表 1 样地1987年基本情况
Table 1. The characteristics of experimental stands established plot
样地号
Plot number面积
Area/hm2海拔
Elavation/m坡向
Aspect坡度
Slope平均胸径
The mean diameter/cm公顷株数
The stem number/(N·hm−2)公顷断面积
Basal area per hectare/(m2·hm−2)301 0.077 5 760 东北 10 14.93 955 16.83 302 0.077 5 760 东北 10 14.71 1 572 26.69 303 0.13 760 东北 10 14.26 1 098 17.64 304 0.097 5 760 东北 10 15.88 883 17.56 305 0.2 780 西 18 15.07 1 158 20.64 306 0.2 780 东北 7 13.66 2 008 29.42 307 0.2 780 西 18 15.02 1 153 20.50 308 0.2 780 东北 10 15.82 846 16.39 309 0.25 660 西北 6 15.61 1 189 22.86 310 0.25 670 西北 10 16.18 860 17.74 311 0.25 670 西北 6 17.20 833 19.39 312 0.25 680 西北 10 15.49 914 17.30 315 0.112 5 660 北 7 13.58 1 694 24.44 316 0.1 645 北 7 14.87 1 127 19.66 317 0.1 615 东北 7 13.51 1 286 18.65 318 0.112 5 610 东北 7 14.39 919 15.03 319 0.1 605 东北 9 15.17 820 14.84 320 0.1 600 东北 9 13.65 1 670 24.41 表 2 Cox比例风险函数模型模拟结果
Table 2. The result of Cox proportional hazard model
协变量
Covariatevariable模型1(M1)
Model 1模型2(M2)
Model 2模型3(M3)
Model 3估计值(标准差)
Estimate result(Standard error)P值
P value估计值(标准差)
Estimate result(Standard error)P值
P value估计值(标准差)
Estimate result(Standard error)P值
P value单木初始胸径
Initial DBH/d−0.052 7(0.007 6) <0.000 1 −0.077 8(0.012 4) <0.000 1 −0.089 5(0.006 5) <0.000 1 大于对象木断面积(BAL)
Basal area of the trees larger
than the subject tree/(m2·hm−2)0.104 7(0.021 1) <0.000 1 0.056 4(0.048 5) 0.244 7 初始林分公顷株数
Initial stem number/(N·hm−2)0.656 5(0.066 4) <0.000 1 0.535 8(0.311 2) 0.085 2 Wald指标
Wald value304.078 9 <0.000 1 528.049 0 <0.000 1 523.407 5 <0.000 1 AIC 21 164.6 20 944.6 20 948.8 BIC 21 180.3 20 960.3 20 964.5 −2LogL 21 158.6 20 938.6 20 942.8 LRT M2/M1LRT=220($p < 0.001$) M3/M2LRT=4.2($p > 0.05$) -
[1] Hann D W. Wang C H. Mortality equation for individual trees in the mixed conifer zone of southwest oregon[M]. Forest Research Laboratory, Oregon State University, Corvallis, Research Bulletin, 1990. 67, 17 . [2] Adame P, del Rio M, Canellas I. Modeling individual-tree mortality in Pyrenean oak (Quercus pyrenaica Willd.) stands[J]. Ann For Sci, 2010, 67(8): 810-810. doi: 10.1051/forest/2010046 [3] Vanoni M, Bugmann H, Nötzli M, et al. Drought and frost contribute to abrupt growth decreases before tree mortality in nine temperate tree species[J]. For Ecol Manage, 2016, 382(15): 51-63. [4] Thapa R, Burkhart H E. Modeling stand-level mortality of Loblolly pine (Pinus taeda L.) using stand, climate, and soil variables[J]. For Sci, 2014, 61(5): 834-846. [5] Moser J W. Dynamics of an uneven-aged forest stand[J]. For Sci, 1972, 18(3): 184-191. [6] Hamilton Jr D A. Event Probability Estimated by Regression[M]. USDA Forest Service Res Pap. 1974, INT-152. [7] Monserud A R. Simulation of forest tree mortality[J]. For Sci, 1976, 22(4): 438-444. [8] Zhao D, Borders B, Wang M, et al. Modeling mortality of second-rotation loblolly pine plantations in the Piedmont/ Upper Coastal Plain and Lower Coastal Plain of the southern United States[J]. For Ecol Manage, 2007, 252(1-3): 132-143. doi: 10.1016/j.foreco.2007.06.030 [9] Yang Y, Huang S. A generalized mixed logistic model for predicting individual tree survival probability with unequal measurement intervals[J]. For Sci, 2013, 59(2): 177-187. [10] Boeck A, Dieler J, Biber P, et al. Predicting tree mortality for European beech in southern Germany using spatially explicit competition indices[J]. For Sci, 2014, 60(4): 613-622. [11] Woodall C W, Grambsch P L, Thomas W. Applying survival analysis to a large-scale forest inventory for assessment of tree mortality in Minnesota[J]. Ecol Model, 2005, 189(3): 199-208. [12] Eerikainen K, Miina J, Valkonen S. Models for the regeneration establishment and the development of established seedlings in uneven-aged, Norway spruce dominated forest stands of southern Finland[J]. For Ecol Manage, 2007, 242(2-3): 444-461. doi: 10.1016/j.foreco.2007.01.078 [13] Allison P D. Survival Analysis Using SAS: A Practical Guide[M].Second ed. SAS Institute Inc.Gary, NC, 2010, [14] Waters W E. Life-table approach to analysis of insect impact[J]. J For, 1969, 67(5): 300-304. [15] Fan Z F, Kabrick J M, Shifley S R. Classification and regression tree based survival analysis in oak-dominated forests of Missouris Ozark highlands[J]. Can J For Res, 2006, 36(7): 1740-1748. doi: 10.1139/x06-068 [16] Von Gadow K, Kotze H, Seifert T, et al. Potential density and tree survival: an analysis based on South African spacing studies[J]. Southern Forests, 2014, 77(2): 1-8. [17] Uzoh F C C, Mori S R. Applying survival analysis to managed even-aged stands of ponderosa pine for assessment of tree mortality in the western United States[J]. For Ecol Manage, 2012, 285(12): 101-122. [18] Yang Y, Titus S J, Huang S. Modeling individual tree mortality for white spruce in Alberta[J]. Ecol Model, 2003, 163(3): 209-222. doi: 10.1016/S0304-3800(03)00008-5 [19] Allison P D. Survival Analysis Using the SAS System, APractical Guide[M]. SAS Institute, Cary, NC, 1995. [20] Lawless J F. Statistical Models and Methods for Lifetime Data[M]. New York: John Wiley and Sons, 2003. [21] Cox D R. Regression models and life tables[J]. J Roy Stat Soc, Ser. B, 1972, 20: 187-220. [22] Wunder J, Brzeziecki B, Zybura H, et al. Growth-mortality relationships as indicators of life-history strategies: a comparison of nine tree species in unmanaged European forests[J]. Oikos, 2008, 117(6): 815-828. doi: 10.1111/j.0030-1299.2008.16371.x [23] Hurst J M, Stewart G H, Perry G L, et al. Determinants of tree mortality in mixed old-growth Nothofagus forest[J]. For Ecol Manage, 2012, 270(2): 189-199. [24] Timilsina N, Staudhammer C L. Individual tree mortality model for Slash pine in Florida: A mixed modeling approach[J]. South J Appl For, 2012, 36(4): 211-219. doi: 10.5849/sjaf.11-026 [25] Wu H, Franklin S B, Liu J M, et al. Relative importance of density dependence and topography on tree mortality in a subtropical mountain forest[J]. For Ecol Manage, 2017, 384(2): 169-179. [26] Moore J A, Hamilton Jr D A, Xiao Y, et al. Bedrock type significantly affects individual tree mortality for various conifers in the inland Northwest, USA[J]. Can J For Res, 2004, 34(1): 31-42. doi: 10.1139/x03-196 [27] 姜晶梅. 医学实用多元统计学[M]. 北京: 科学出版社, 2014. [28] Rawlings J O, Pantula S G, Dickey D A. Applied Regression Analysis: A Research Tool[M]. 2nd edn. Springer, New York. 1998. [29] Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction[M]. Springer, New York. 2001. [30] Burnham K P, Anderson D R. Model Selection and Multi-model Inference: A Practical Information-theoretic Approach [M]. 2nd edn, Springer, 2002, New York. [31] 李春明. 基于两层次线性混合效应模型的杉木林单木胸径生长量模型[J]. 林业科学, 2012, 48(3):66-73. doi: 10.11707/j.1001-7488.20120311 [32] Yaussy D A, Iverson L R, Matthews S N. Competition and climate affects US hardwood-forest tree mortality[J]. For Sci, 2012, 59(4): 416-430. [33] Csilléry K, Seignobosc M, Lafond V. Estimating long-term tree mortality rate time series by combining data from periodic inventories and harvest reports in a Bayesian state-space model[J]. For Ecol Manage, 2013, 292(2): 64-74. [34] Nesmith Jonathan C B, Das A J, O'Hara K L, et al. The influence of prefire tree growth and crown condition on postfire mortality of sugar pine following prescribed fire in Sequoia National Park[J]. Can J For Res, 2015, 45(7): 910-919. doi: 10.1139/cjfr-2014-0449 -



 下载:
下载: