-
杉木(Cunninghamia lanceolata(Lamb.)Hook.)是我国主要造林树种之一[1-4],关于杉木树高-胸径模型,很多学者都开展过研究,但多为小区域建模。沈子奕等[5]以江西省青原山杉木人工林为研究区,在基础模型上构建了混合效应模型,结果表明,加入地形因子的混合效应模型能够更好的拟合该地区树高-胸径关系。魏晓慧等[6]利用福建省三明市将乐县国有林场的杉树人工林调查数据,对Richards方程进行拟合,得出Richards模型能够提高拟合精度的结果。黄其城[7]选择4个常用的相对树高曲线模型对福州市8个国有林场60片伐区的树高-胸径调查数据进行拟合,最终确定Richards函数变形固定参数模型作为杉木相对树高曲线的最优模型。近年来,在树高-胸径模型的构建中逐渐加入了如海拔、林分密度、土壤条件、立地条件等随机效应,用混合模型的方法来提高模型的拟合精度[8-12],但是这些模型大多都基于林场等小区域建模,在实际应用时需要重新求解随机效应参数,限制了模型的应用。在某一地区建立的模型,难以推广到其他地区,并且仍有杉木非核心分布区树高-胸径模型缺失,因此建立大区域乃至全国大尺度杉木树高-胸径模型显得尤其重要。目前,大区域的杉木树高-胸径模型在我国的研究还较少,如覃阳平等[13]选用Richards等15种树高-胸径模型作为候选模型,建立了云南省5个针叶树种的树高-胸径模型,其中杉木的最优模型为Hossfeld方程。李海奎等[14]分别采用树高分级和未分级的方法,建立了杉木等6个我国主要树种的树高曲线模型,结果表明分级建模方法的精度显著优于未分级建模。
因此,为推进我国杉木大尺度区域建模方面的研究,本研究基于第六次、第七次全国森林资源连续清查固定样地数据,以全国15个省份的杉木人工林为研究对象,选用18种常见的生长模型作为候选模型,分别拟合杉木树高胸径的关系,分省区建立杉木人工林最优平均木树高-胸径模型。
-
杉木人工林主要分布于我国的15个省区,分别为江苏、安徽、河南、浙江、福建、江西、湖北、湖南、广东、广西、重庆、四川、陕西、贵州和云南,为了便于应用,本研究分省区建立杉木树高-胸径模型,但由于一些省份杉木样地数据过少,参考张英凯等[15]杉木分布区分组的结果,对低于100个观测数据的省份进行合并处理。江苏省和安徽省均位于长江中下游平原,河南省的杉木样地分布于该省东南部,紧邻安徽省杉木分布区,且3省的杉木分布区气候都属亚热带季风气候,因此将江苏、安徽和河南3省数据合并处理(以下简称苏徽豫),一同建模。陕西省杉木样地主要分布在该省秦岭南部地区,紧邻重庆市北部的杉木样地,因此将陕西省数据与重庆市数据合并处理(以下简称渝陕),其余各省区单独处理。
-
所用数据来自于第六次、第七次一类清查杉木人工林固定样地数据的树高调查表,每个固定样地选取3~5株胸径接近样地平均胸径的树木测定其树高,剔除不完整的样本,最终总样本数为23 239个平均木单株树高-胸径数据。详细的数据统计量如表1所示。
省区
Provincial area样本数
Number of
trees变量
Variable平均值
Mean标准差
SD最小值
Min.最大值
Max.苏徽豫 4 230 D 10.0 2.5 5.0 22.7 H 7.4 2.0 2.5 15.4 浙江 3 712 D 10.8 3.3 5.0 28.0 H 7.1 2.2 2.3 19.4 福建 4 962 D 11.9 3.8 5.0 30.0 H 9.0 3.1 1.3 21.6 江西 2 901 D 10.3 2.9 5.0 26.0 H 7.4 2.3 1.4 17.8 湖北 188 D 14.0 5.6 5.2 33.2 H 11.1 4.3 3.8 21.0 湖南 3 591 D 11.4 3.4 5.0 27.5 H 8.5 2.5 2.3 21.0 广东 1 308 D 10.7 3.5 5.0 29.7 H 8.0 2.6 2.2 17.1 广西 192 D 12.5 3.6 5.2 22.5 H 10.3 3.3 4.0 19.3 四川 258 D 12.1 3.8 5.3 26.7 H 9.4 3.1 3.2 21.6 贵州 815 D 12.0 3.9 5.0 29.7 H 8.7 3.0 2.9 23.0 云南 596 D 12.1 4.7 5.1 34.7 H 8.6 3.3 2.8 19.3 渝陕 486 D 12.2 3.5 5.8 26.5 H 9.4 2.9 2.7 19.0 Table 1. Summary statistics for diameter at breast height (D) and tree height(H) of Cunninghamia lanceolata
-
根据前人的研究经验[14,16-18],采用常见的18个线性和非线性模型作为候选模型来拟合杉木的树高-胸径关系,探讨杉木各省区最适宜的树高曲线形式,候选树高-胸径模型的具体表达式如表2所示。
模型
序号
Models
No.模型
类型
Model
types参数个数
Number of
parameters方程名称
Equation
name模型表达式
Height-diameter
function1 线性
模型2 $ H=a + b\mathrm{log}D $ 2 $ H=\frac{1}{a + b{D}^{-1}} $ 3 3 $ H=a + bD + c{D}^{2} $ 4 非线性
模型2 幂函数 $ H=1.3 + a{D}^{b} $ 5 Wykoff $ H=1.3 + {\rm {e}}^{a + \frac{b}{D + 1}} $ 6 Bates方程 $ H=1.3 + \frac{aD}{b + D} $ 7 Schumacher $ H=1.3 + a{\rm {e}}^{\frac{b}{D}} $ 8 双曲线 $ H=1.3 + a{\left(\frac{D}{1 + D}\right)}^{b} $ 9 3 Richard $ H=1.3 + a{\left(1-{\rm {e}}^{-bD}\right)}^{c} $ 10 Weibull $ H=1.3 + a\left(1-{\rm {e}}^{-b{D}^{c}}\right) $ 11 Logistic $ H=1.3 + \frac{a}{1 + b{\rm {e}}^{-cD}} $ 12 Korf $ H=1.3 + a{\rm {e}}^{-\frac{b}{{D}^{c}}} $ 13 Gompertz $ H=1.3 + a{\rm {e}}^{-b{\rm {e}}^{-cD}} $ 14 Hossfeld $ H=1.3 + \frac{a}{1 + {b}^{-1}{D}^{-c}} $ 15 唐守正树高曲线方程 $ H=1.3 + a + \frac{b}{D + c} $ 16 Mitscherlich $ H=1.3 + a\left(1-b{\rm {e}}^{-cD}\right) $ 17 Ratkowsky $ H=1.3 + a{\rm {e}}^{\frac{-b}{D + c}} $ 18 柯列尔 $ H=1.3 + a{D}^{b}{\rm {e}}^{-cD} $ 注:H为树高值(单位:m),D为胸径(单位:cm);a,b,c为参数。
Notes: H is tree height (unit : m), D is diameter at breast height (unit : cm); a, b, c are parameters.Table 2. Eighteen kinds of height-diameter curve model for candidate
-
模型的评价主要利用决定系数(R2)、平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)和平均预估误差(MPE)5种评价指标,分析残差分布图,并考虑模型各参数的生物学意义以及参数的取值范围是否合理,以此来确定各省区拟合效果最优的模型。R2的值越接近1,MAE、MRE、RMSE和MPE的值越小,说明该模型拟合精度越高[6,19]。
在确定各省区最优模型后,模型验证部分采用5折交叉验证法,具体步骤为:首先将全部数据平均分成5份,每次从5份数据中拿出4份用来建模,剩下的1份作为验证数据,重复进行5次,共建模5次得到5个子模型,应用5个子模型的交叉检验估计值计算各误差指标,依据MAE、MRE、RMSE和MPE越小越好的原则,来评价选择的各省区最优模型的预测能力。
-
最优模型的选取遵循模型拟合精度最高同时误差最小的规则,综合权衡R2,MAE,MRE、RMSE和MPE 5个指标,以及模型参数的取值是否符合生物学规律,得出各省区最优树高-胸径模型。各省区最优平均木树高-胸径模型建模结果和误差分析见表3。可以看出,各省区最优模型并不相同,最优模型以模型16(Mitscherlich方程)为主,各省区的拟合结果均具有较高的精度,每个省区最优模型的R2介于0.602~0.807之间, MAE介于0.94~1.53 m之间,MRE介于−2.93%~−4.72%之间,RMSE介于1.23~2.00 m之间,MPE介于0.50%~2.77%之间。江苏省、安徽省和河南省的MAE最小,各省的MRE均小于±5%,RMSE均小于2.00 m,MPE均小于3%。其中湖北省最优模型拟合结果精度最高,最优模型为模型11(Logistic方程),R2达到0.807,MAE,MRE,RMSE和MPE分别为1.53 m,−3.33%,1.89 m,2.49%;广东省最优模型的拟合结果精度最低,R2为0.602,MAE,MRE,RMSE和MPE分别为1.29 m,−4.38%,1.66 m,1.13%。
省区
Provincial area最优模型编号
Best model No.最优模型
Best model评价指标
Evaluation indicatorsR2 MAE/m MRE/% RMSE/m MPE/% 苏徽豫 14 Hossfeld 0.618 0.94 −2.93 1.23 0.50 浙江 16 Mitscherlich 0.646 1.01 −3.47 2.00 0.61 福建 14 Hossfeld 0.712 1.29 −4.00 1.69 0.52 江西 16 Mitscherlich 0.657 1.05 −3.47 1.37 0.67 湖北 11 Logistic 0.807 1.53 −3.33 1.89 2.49 湖南 16 Mitscherlich 0.619 1.18 −3.27 1.54 0.59 广东 8 双曲线 0.602 1.29 −4.38 1.66 1.13 广西 16 Mitscherlich 0.638 1.50 −3.70 1.99 2.77 四川 16 Mitscherlich 0.704 1.28 −3.03 1.68 2.20 贵州 13 Gompertz 0.641 1.37 −4.42 1.81 1.43 云南 16 Mitscherlich 0.753 1.22 −3.48 1.64 1.54 渝陕 16 Mitscherlich 0.611 1.44 −4.72 1.85 1.76 Table 3. Error analysis of the optimal average tree height - diameter model in each province
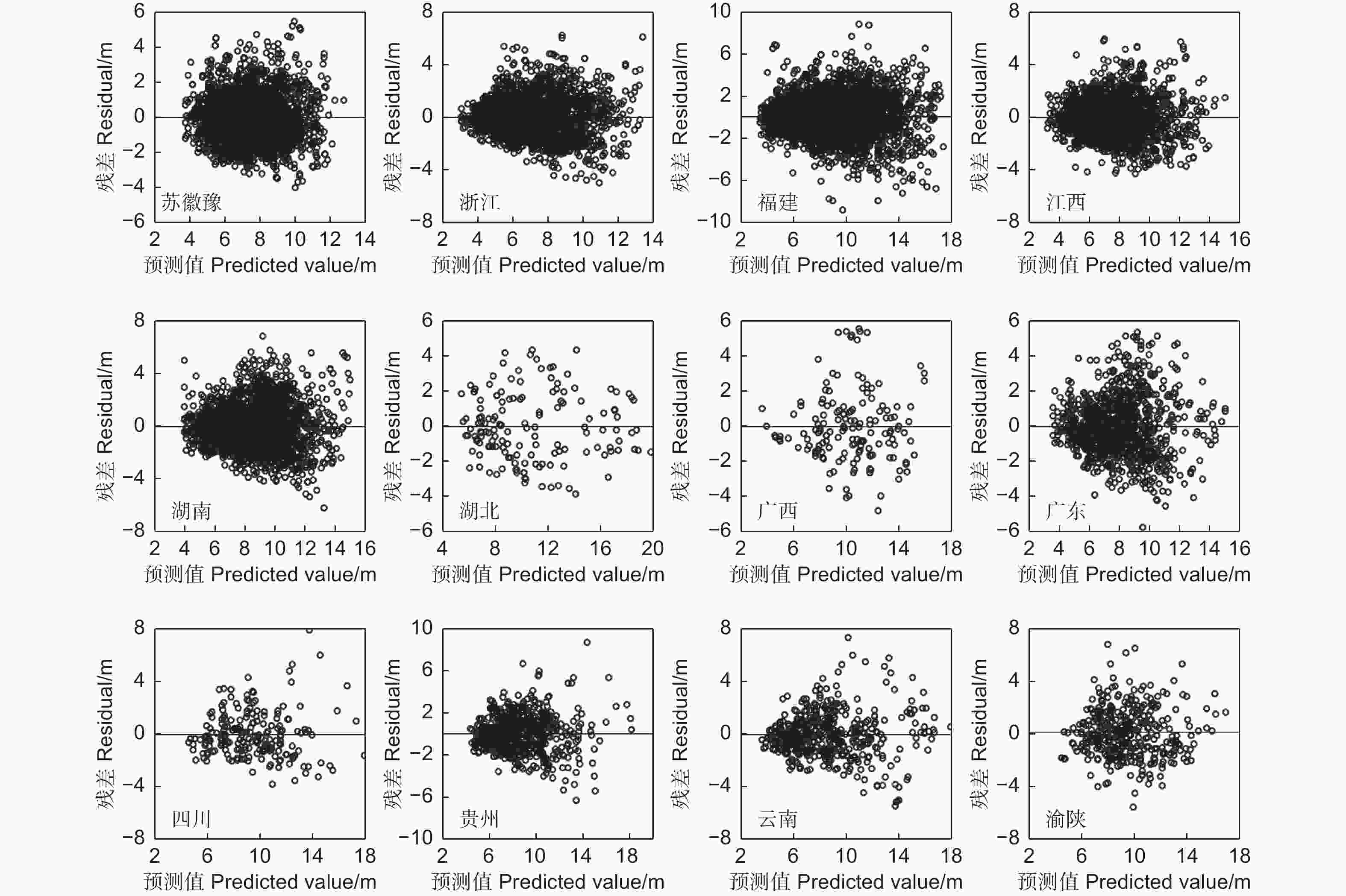
15个省区最优模型的树高预测值-残差的分布如图1所示,残差点较为平均地落在残差值为0的标准线的上下两端,大部分都分布在 ±4的残差值之内,也有少数残差值较大的样本,但并无明显的异质性,表明模型的拟合效果较好,能够应用于实际的拟合预测。
-
为检验模型的适用性,采用5折交叉验证法对各省区5次建模的最优模型预测能力进行检验,用5个子模型的交叉检验估计值计算相关误差指标,得到各省区的误差精度指标以及建模结果见表4。从表4可以看出,MAE在0.94~1.57 m之间,MRE在−2.93%~−4.65%之间,RMSE在1.23~2.00 m之间,MPE在0.41%~2.77%之间,各省区最优模型的检验结果大体与建模数据的分析结果一致,同时所有模型的MRE在± 5%以内,满足精度要求,MAE均在2.00 m以内,RMSE均小于或等于2.00 m,MPE均小于3%,说明模型预测效果好,所有模型的误差较小,得出的15个省区的最优树高-胸径模型有较强的适用性,可以在实际中应用。
省区
Provincial area模型表达式
Model fitting results评价指标
Evaluation indicatorsMAE/m MRE/% RMSE/m MPE/% 苏徽豫 $H=1.3 + \frac{14.73}{1 + {0.009\;693}^{-1}{D}^{-1.884} }$ 0.94 −2.93 1.23 0.50 浙江 $ H=1.3 + 15.15\left(1-1.212{\rm {e}}^{-0.064\;56D}\right) $ 1.02 −3.47 1.34 0.41 福建 $ H=1.3 + \frac{24.54}{1 + {0.006\;737}^{-1}{D}^{-1.714}} $ 1.29 −3.99 1.69 0.52 江西 $ H=1.3 + 19.18\left(1-1.175{\rm {e}}^{-0.054\;23D}\right) $ 1.05 −3.46 1.37 0.67 湖北 $ H=1.3 + \frac{19.48}{1 + 10.31{\rm {e}}^{-0.169\;6D}} $ 1.57 −3.05 1.93 2.54 湖南 $ H=1.3 + 19.51\left(1-1.106{\rm {e}}^{-0.050\;29D}\right) $ 1.18 −3.26 1.54 0.59 广东 $ H=1.3 + 20.23{\left(\frac{D}{1 + D}\right)}^{11.89} $ 1.29 −4.35 1.66 1.13 广西 $ H=1.3 + 21.12\left(1-1.248{\rm {e}}^{-0.064\;19D}\right) $ 1.51 −3.49 2.00 2.77 四川 $ H=1.3 + 29.94\left(1-1.077{\rm {e}}^{-0.032\;76D}\right) $ 1.29 −3.11 1.70 2.25 贵州 $ H=1.3 + 20.63{\rm {e}}^{-2.908{\rm {e}}^{-0.087\;03D}} $ 1.37 −4.41 1.82 1.44 云南 $ H=1.3 + 20.83\left(1-1.190{\rm {e}}^{-0.052\;08D}\right) $ 1.23 −3.47 1.65 1.55 渝陕 $ H=1.3 + 23.95\left(1-1.111{\rm {e}}^{-0.043\;44D}\right) $ 1.45 −4.65 1.86 1.77 Table 4. Optimal average tree height - diameter model in each province and cross-validation results
-
树高-胸径模型是立地质量评价和反演复杂模型的基础。不同于以往的杉木小区域建模,本研究建立了杉木人工林分布的各省区的大尺度的树高生长模型。小区域建模的研究范围一般为林场或区县,数据量较少,受环境差异影响较小,虽然适用范围有限,但模型精度相对较高,R2通常在0.8以上[20-23]。大尺度建模研究区域一般在整个省乃至全国范围内,所用数据量较大,适用范围广泛,但省内或全国范围内各地环境存在差异,因此建模精度相对较低,R2通常分布在0.6~0.8之间[14,18,24]。本研究建立的各省区模型R2在0.610~0.834之间,平均值为0.679,建模精度在上述有关学者的大区域杉木建模精度范围内,因此本研究建立的各省区的杉木树高-胸径生长模型可以预测不同径阶杉木的树高情况。本研究评价指标中,平均相对误差(MRE)没有绝对值,因此是存在正负的,正值表示实测值大于预测值,负值表示实测值小于预测值,本研究MRE均为负数,表明拟合模型的预测结果大部分都大于实测值,但MRE整体均分布在±5%之间,结果符合精度要求。
交叉验证在模型检验中应用广泛,操作简便,本研究验证,部分采用了5折交叉验证法,充分利用样本数据,能够更准确地检验选出的最优模型的预测能力,但是交叉验证的折数是可以改变的,不同折数不仅决定着建模和检验样本的多少,还影响着误差指标的结果和计算的复杂程度,本研究为便于计算,选用了5折交叉验证法,在未来的研究中,可尝试10折交叉验证或其他验证方法进行验证。
本研究只考虑了杉木树高与胸径的关系,只有胸径一个自变量,应用范围较广泛。同时,杉木树高的生长情况还受多种因素影响,如海拔高度、林分密度、气象条件、立地条件、经营目标、抚育间伐等 [25-27],未来可以尝试建立包含多种林分因子(包括因子间的相互作用)的广义树高-胸径模型,也许可以进一步提高模型的精度。由于本研究采用了两期数据,存在相关性,未采用混合效应模型,因为混合效应模型需要进行新的随机参数估计,会限制其在实际中的应用。另外,本研究为便于模型的实际应用,按行政区划进行建模,未比较不同省份之间回归模型的差异显著性,将来可在差异比较的基础上,将差异不显著的省份合并建模,尝试利用杉木产区划分进行建模。
-
本研究基于第六次、第七次全国森林一类清查固定样地数据,以杉木人工林分布的15个省区为研究区,利用18种基础生长方程,分别对各省区杉木平均木树高-胸径数据进行拟合,然后根据模型的决定系数(R2)、平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)和平均预估误差(MPE)这5个评价指标,并参考树高预测值-残差分布图,最终决定各省区适宜的模型,建立了全国杉木各省区平均木树高-胸径关系模型。结果表明:各省区的最优平均木树高-胸径模型不尽相同,模型的决定系数R2在0.602~0.807之间, MAE在0.94~1.53 m之间,MRE在−2.93%~−4.72%之间,RMSE在1.23~2.00 m之间,MPE在0.50%~2.77%之间。经检验,模型拟合效果较好,参数取值范围合理,对于杉木树高-胸径的拟合效果较好,可以作为全国各省区基本的最优杉木人工林平均木树高-胸径模型。
Average Tree Height-Diameter Models of Cunninghamia lanceolata in China Based on Continuous Forest Inventory Plot Data
- Received Date: 2022-06-20
- Accepted Date: 2022-07-15
- Available Online: 2023-02-20
Abstract:




 DownLoad:
DownLoad: