-
光合作用是植物(包括光合细菌)吸收光能并转换为化学能合成有机物并且储藏的生物过程,是地球生态系统一切生命活动的物质基础和能量来源。光合作用与光照、温度、水、热等环境因子密切相关,在诸多环境因子中,光是光合作用的主导因子[1]。净光合速率是植物光合作用强弱的直接体现,净光合速率和光合有效辐射之间通过光响应曲线建立关系[2],为了定量研究光照强度与净光合速率之间的关系,光合研究工作者建立了许多两者之间关系的模型,目前经常使用的有直角双曲线模型、非直角双曲线模型、直角双曲线修正模型和指数模型。其中直角双曲线模型、非直角双曲线模型、指数模型在定义域范围内是单调递增的,最大的缺点就是不存在光饱和点[3-5],而直角双曲线修正模型的函数存在极值,可以直接计算出光饱和点[6-7],所以选择适宜的模型进行光合参数的计算以及光合效应的评价非常重要。
毛竹(Phyllostachys edulis (Carr.) H. de Lehaie)隶属禾本科(Poaceae)竹亚科(Bambusoideae)刚竹属(Phyllostachys Sieb. et Zucc.),是我国最为重要的经济竹种,也是竹产区农民家庭经济收入的重要来源以及区域社会经济发展的重要资源。然而,目前存在毛竹林产品(竹材、竹笋)产量提高空间小、竹产品市场疲软、竹林经营效益下降、竹农经营毛竹林积极性降低等问题,迫切需要采取有效的技术措施或经营模式来切实提高毛竹林经营效益。其中,采取毛竹与林下生态适应性强、经济价值高、市场需求大的经济植物进行复合经营,构建操作简便、投入少、见效快的复合经营模式是条有效途径,如具有药用价值和林地培肥作用的固氮植物苦参(Sophora flavescens Alt.)和决明(Catsia tora Linn.)与毛竹的复合经营。苦参隶属豆科(Leguminosae)槐属(Sophora Linn.),具有清热燥湿、杀虫利尿等功效,可用于治疗热痢、便血、黄疸闭尿、赤白带下、阴肿阴痒、湿疹、皮肤瘙痒等病症,还具有抗纤维化、抗肿瘤、抗病毒等多种药理活性,也可用于生物农药生产。决明隶属豆科决明属(Cassia Linn.),是中国传统的中药材,具有清肝火、祛风湿、益肾明目等功效,还含有多种维生素、丰富的氨基酸、脂肪和碳水化合物等,具有很好的保健功能[8]。
自上世纪90年代以来,国内外竹类研究者针对毛竹林经营中存在的主要问题,开展了毛竹林下植被群落结构及其人工干扰效应[9-10]、林下植被物种多样性对毛竹林土壤性状的影响[11]、毛竹林下植物复合经营[12-14]等研究,而有关光响应方面的研究很少,用4曲线拟合方法对毛竹林下苦参和决明光响应曲线的研究尚未见报道。为此,本研究以不同立竹密度的毛竹林下种子播种的苦参和决明幼苗为试材,采用直角双曲线模型、非直角双曲线模型、直角双曲线修正模型和指数模型进行光响应曲线拟合,分析比较苦参和决明的光响应生理参数,筛选出适宜的毛竹林下苦参和决明光响应拟合模型,探讨苦参和决明对不同立竹密度毛竹林下光环境的适应规律,为毛竹林下苦参和决明的复合经营提供理论参考。
-
试验地位于浙江省江山市(118°30′20″118°30′30″ E,28°22′10″28°22′30"N)保安乡,处于浙、闽、赣三省交界处。属中亚热带季风气候,四季分明,雨热同期,雨水充沛,年降水量1 6502 200 mm,相对湿度85%95%,年平均气温17.1 ℃,年平均日照时数2 063.3 h,年平均无霜期253 d。土壤主要为红壤。试验地毛竹林资源丰富,是江山市毛竹主要产出乡镇,面积800多hm2,多为纯林,实施笋材两用林经营方式,经营较为粗放,实行季节性伐竹和留笋养竹,未采取过林地恳复、施肥等措施。
-
2016年1月上旬在试验地选择立地条件和经营措施一致、当年为春笋出笋小年的毛竹林,采用伐除老竹、弱小竹的方式进行立竹密度调整,设置成3种立竹密度的试验毛竹林,分别为低密度(D1,1 600±200株·hm-2)、中密度(D2,2 400±200株·hm-2)、高密度(D3,3 200±200株·hm-2),每种试验林面积不少于0.4 hm2。试验林坡向东南向,立竹平均胸径为10.8±1.2 cm,试验林间无显著差异。于2016年4月上旬在同一坡位的试验毛竹林中进行带状播种苦参和决明,播种前对林地进行清理,清除林下植被,沿等高线按3.0 m行距开浅沟,将预处理过的苦参(4045 ℃温水浸泡1012 h)和决明(60 ℃温水浸泡2 h)分别均匀混合草木灰撒入沟内,后覆土。试验林苦参、决明种子用量分别为15.0、7.5 kg·hm2左右。6—7月人工去除播种带的杂草。
2016年7月下旬选择晴朗的天气,于8:00—11:00在不同立竹密度的试验毛竹林下随机选择健康生长的苦参和决明各3株(株高、地径见表 1),作为3个重复,每株选择中上部叶片完整、中等大小、颜色正常的叶片用Li-6400光合作用分析仪(Licor Inc.,Lincoln,USA)进行光响应曲线测定,手动设置Li-6400的人工光源(Li-6400-02B红蓝光源)光照强度为2 000、1 800、1 500、1 200、1 000、800、700、600、500、300、200、150、100、50、0 μmol·m-2·s-1。为保证其它环境因子稳定且适宜,观测过程中,将叶温设置为25℃,相对湿度为60%,大气CO2浓度为400 μmol·mol-1。
表 1 不同立竹密度毛竹林下苦参和决明幼苗的株高和地径
Table 1. The height and stem basal diameter of seedling of S. flavescens and C. tora under different density of moso bamboo
植物
Plants株高Height/cm 地径Basal Diameter/mm D1 D2 D3 D1 D2 D3 苦参S. flavescens 16.49±1.40a 12.69±1.49b 12.01±1.36b 10.12±1.08a 7.16±0.75b 6.93±0.0b 决明C. tora 30.13±2.37a 22.48±2.22b 20.75±2.09b 10.33±1.13a 9.95±1.08ab 9.22±0.98b -
$ {P_n}(I) = \frac{{\alpha I{P_{n{\rm{max}} }}}}{{\alpha I + {P_{n{\rm{max}} }}}} - {R_d} $
(1) 式中,Pn(I)为净光合速率,I为光合有效辐射(μmol·m-2·s-1),α为初始量子效率(μmol·μmol-1),Pnmax为最大净光合速率,Rd为暗呼吸速率。
-
$ \begin{array}{l} {P_n}(I) = \frac{{\alpha I + {P_{n{\rm{max}} }} - \sqrt {\left( {\alpha I + {P_{n{\rm{max}} }}} \right)2 - 4\theta \alpha I{P_{n{\rm{max}}}}} }}{{2\theta }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {R_d} \end{array} $
(2) 式中,θ为曲线的曲率,Pn(I)、α、I、Pnmax、Rd同上。
-
$ {P_n}(I) = \alpha \frac{{I - \beta I}}{{I + \gamma I}}I - {R_d} $
(3) 式中,β和γ为系数,Pn(I)、α、I、Rd同上。
-
$ {P_n}(I) = {P_{n{\rm{max}} }}\left( {1 - {e^{ - \alpha I/{P_{n{\rm{max}}}}}}} \right) - {R_d} $
(4) 式中,Pn(I)、Pnmax、α、I、Rd同上。
-
将测定的苦参和决明的净光合速率(Pn)值求平均值,用Photosynthesis1.0分别进行4个模型的拟合,得到不同立竹密度的毛竹林下苦参和决明4个模型各个光照强度下的拟合值,用OriginPro 8.0以光合有效辐射(PAR)为横坐标,净光合速率(Pn)为纵坐标,绘制不同模型的光响应曲线图。选择出PAR为2 000、1 800、1 500、1 200、800、700、600、500、300、150、100、0 μmol·m-2·s-1对应的拟合值,并计算出各模型PAR为2 000、1 000、400、200、50 μmol·m-2·s-1对应的Pn值,作为预测值,用于检验4个模型的精确度。为了能够更好的检验拟合和预测的精确度,采用均方误差(MSE)和平均绝对误差(MAE) 2个参数来判定。
-
由表 2可以看出,在不同立竹密度的毛竹林下,由光响应曲线模型拟合苦参和决明所得的均方误差(MSE)、平均绝对误差(MAE)几乎都比预测值小,说明这些模型的拟合效果较好。苦参在D1和D2立竹密度的毛竹林下4种模型拟合的MSE、MAE大小顺序为直角双曲线模型 > 非直角双曲线模型 > 指数模型 > 直角双曲线修正模型,预测的MSE和MAE大小顺序为指数模型 > 直角双曲线模型 > 直角双曲线修正模型 > 非直角双曲线模型,在D3立竹密度毛竹林下拟合和预测的MSE、MAE值的大小顺序均为直角双曲线模型 > 指数模型 > 非直角双曲线模型 > 直角双曲线修正模型。决明在D1立竹密度毛竹林下4种模型拟合和预测的MSE、MAE大小顺序为直角双曲线模型 > 指数模型 > 非直角双曲线模型 > 直角双曲线修正模型,在D2立竹密度和高立竹密度毛竹林下拟合的MSE、MAE大小顺序为直角双曲线模型 > 非直角双曲线模型 > 指数模型 > 直角双曲线修正模型,预测的MSE、MAE在D2立竹密度毛竹林下为直角双曲线模型 > 指数模型 > 非直角双曲线模型 > 直角双曲线修正模型,D3立竹密度毛竹林下为指数模型 > 直角双曲线模型 > 非直角双曲线模型 > 直角双曲线修正模型。在不同立竹密度的毛竹林下苦参和决明拟合的MSE和MAE均是直角双曲线修正模型最小,直角双曲线模型最大,预测的MSE和MAE直角双曲线模型明显大于直角双曲线修正模型。
表 2 试验毛竹林下苦参和决明幼苗4个光响应拟合模型的MSE和MAE
Table 2. The MSE and MAE of seedling of S. flavescens and C. tora under test moso bamboo estimated by four models
植物
Plants立竹密度
Bamboo density模型
Model拟合值的MSE
Fitted MSE拟合值的MAE
Fitted MAE预测值的MSE
Test MSE预测值的MAE
Test MSE苦参
S. flavescensD1 直角双曲线模型Rectangle hyperbola 0.879 0.805 0.793 0.780 非直角双曲线模型Non-rectangle hyperbola 0.007 0.066 0.014 0.111 直角双曲线修正模型Modified rectangular hyperbola Model 0.004 0.055 0.065 0.108 指数模型Exponential Model 0.006 0.059 1.005 0.980 D2 直角双曲线模型Rectangle hyperbola 1.409 0.919 0.868 0.0824 非直角双曲线模型Non-rectangle hyperbola 0.019 0.116 0.009 0.072 直角双曲线修正模型Modified rectangular hyperbola Model 0.004 0.051 0.030 0.092 指数模型Exponential Model 0.015 0.101 1.057 1.019 D3 直角双曲线模型Rectangle hyperbola 0.162 0.107 2.679 1.442 非直角双曲线模型Non-rectangle hyperbola 0.011 0.083 0.056 0.163 直角双曲线修正模型Modified rectangular hyperbola Model 0.002 0.034 0.025 0.088 指数模型Exponential Model 0.014 0.102 0.964 0.967 决明C. tora D1 直角双曲线模型Rectangle hyperbola 4.399 1.258 2.924 1.027 非直角双曲线模型Non-rectangle hyperbola 1.041 0.773 1.232 0.787 直角双曲线修正模型Modified rectangular hyperbola Model 0.217 0.313 0.243 0.336 指数模型Exponential Model 1.047 0.779 2.267 1.400 D2 直角双曲线模型Rectangle hyperbola 4.088 1.639 3.746 1.573 非直角双曲线模型Non-rectangle hyperbola 0.053 0.195 0.243 0.335 直角双曲线修正模型Non-rectangle hyperbola 0.007 0.052 0.025 0.099 指数模型Exponential Model 0.051 0.175 0.997 0.901 D3 直角双曲线模型Rectangle hyperbola 1.128 0.880 3.018 1.205 非直角双曲线模型Non-rectangle hyperbola 0.065 0.166 0.859 0.851 直角双曲线修正模型Modified rectangular hyperbola Model 0.036 0.139 0.160 0.668 指数模型Exponential Model 0.060 0.156 3.505 1.686 -
从表 3可以看出,不同立竹密度的毛竹林下,4种模型拟合得到的苦参和决明初始量子效率(α)、最大净光合速率(Pnmax)、暗呼吸速率(Rd)、光补偿点(LCP)存在一定的差异。其中,苦参幼苗4种模型拟合的α值随着立竹密度的增大均呈现倒“Ⅴ”型变化;直角双曲线模型拟合的Pnmax值3个立竹密度下相等,非直角双曲线模型呈“Ⅴ”型变化,直角双曲线修正模型拟合值呈倒“Ⅴ”型变化,指数模型拟合值呈递增趋势;直角双曲线模型拟合的Rd值随着立竹密度增大呈倒“Ⅴ”型变化,其余3种模型拟合值呈递减变化;直角双曲线模型拟合的LCP值随着立竹密度的增大呈倒“Ⅴ”型变化,非直角双曲线模型拟合值逐渐递减,直角双曲线修正模型和指数模型均呈“Ⅴ”型变化。决明幼苗直角双曲线拟合的α值随着立竹密度的增大呈现“Ⅴ”型变化,非直角双曲线模型拟合值逐渐递增,直角双曲线修正模型呈倒“Ⅴ”型变化,指数模型呈递减变化趋势;直角双曲线模型拟合的Pnmax值3个立竹密度下相等,非直角双曲线模型呈倒“Ⅴ”型变化,直角双曲线模型拟合值呈递减趋势,指数模型拟合值呈倒“Ⅴ”型变化;直角双曲线模型拟合的Rd值随着立竹密度增大呈“Ⅴ”型变化,其余3种模型拟合值呈递减变化;直角双曲线模型拟合的LCP值随着立竹密度的增大呈“Ⅴ”型变化,非直角双曲线模型和直角双曲线修正模型拟合值逐渐递减,指数模型均呈递增趋势。另外,只有直角双曲线修正模型可以计算出光饱和点(LSP),并且随着立竹密度的增加,苦参和决明的LSP依次为1 031.197、866.613、745.913、572.100、817.604、735.658 μmol·m-2·s-1。
表 3 试验毛竹林下苦参和决明幼苗4种光响应拟合模型参数
Table 3. The light response physilogical parameters of seedling of S. flavescen and C. tora under test moso bamboo estimated by four models
植物
Plants立竹密度
Bamboo density模型Model α Pnmax Rd LCP LSP 苦参 D1 直角双曲线模型Rectangle hyperbola 0.012 10.000 0 0.003 — S. flavescens 非直角双曲线模型Non-rectangle hyperbola 0.048 5.672 0.677 14.840 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.070 4.845 0.678 10.777 1 031.197 指数模型Exponential Model 0.043 4.745 1.135 30.554 — D2 直角双曲线模型Rectangle hyperbola 0.131 10.000 3.415 40.821 — 非直角双曲线模型Non-rectangle hyperbola 0.051 5.555 0.490 9.898 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.086 5.002 0.493 6.193 866.613 指数模型Exponential Model 0.052 4.898 1.096 23.749 — D3 直角双曲线模型Rectangle hyperbola 0.080 10.000 1.825 27.965 — 非直角双曲线模型Non-rectangle hyperbola 0.043 6.627 0.347 8.125 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.067 4.113 0.367 5.753 745.913 指数模型Exponential Model 0.046 5.992 1.053 25.478 — 决明C. tora D1 直角双曲线模型Rectangle hyperbola 0.251 10.000 5.642 51.745 — 非直角双曲线模型Non-rectangle hyperbola 0.021 3.466 0.776 37.078 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.028 3.612 0.678 26.677 572.100 指数模型Exponential Model 0.034 2.691 1.306 52.912 — D2 直角双曲线模型Rectangle hyperbola 0.005 10.000 0.007 0.139 — 非直角双曲线模型Non-rectangle hyperbola 0.022 3.547 0.670 31.568 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.031 2.920 0.655 24.827 817.604 指数模型Exponential Model 0.022 2.782 1.239 74.436 — D3 直角双曲线模型Rectangle hyperbola 0.094 10.000 5.027 108.123 — 非直角双曲线模型Non-rectangle hyperbola 0.094 2.529 0.276 23.038 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.019 2.464 0.300 17.414 735.658 指数模型Exponential Model 0.017 2.262 1.148 93.390 — -
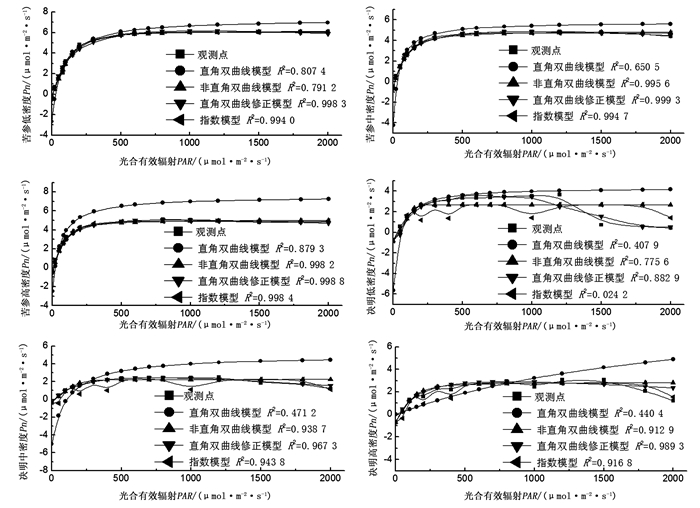
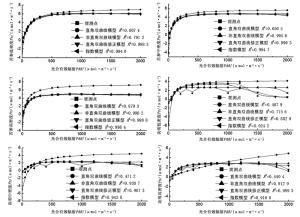
不同立竹密度毛竹林下苦参幼苗净光合速率(Pn)对光强的响应曲线趋一致(图 1),即在一定的光强范围内,净光合速率(Pn)随着光强的增强而增加,但当光强超过光饱和点(LSP)后,净光合速率(Pn)随着光强的增强而降低。但直角双曲线模型拟合得到的曲线偏离观测值较大,并且立竹密度越大相同光照强度下偏离越明显;非直角双曲线模型、直角双曲线修正模型和指数模型拟合曲线与观测值接近,其中直角双曲线修正模型拟合值与观测值最为接近,拟合模型的决定系数R2值均在0.990 0以上,尤其在中立竹密度下更是高达0.999 3。决明幼苗在不同立竹密度毛竹林下4种光合拟合模型拟合曲线规律不明显,其中直角双曲线模型随着光强的增加呈现递增趋势,与观测值偏离明显,拟合决定系数R2值均小于0.5000;非直角双曲线模型和指数模型拟合曲线随着光强的增加先增加后趋于稳定,只有直角双曲线修正模型在光照强度较大时会呈现下降趋势,与实际观测值的变化趋势一致,且在高立竹密度毛竹林下拟合决定系数R2值高达0.989 3。
-
由均方误差(MSE)与平均绝对误差(MAE)值的大小可以判断出拟合值与预测值之间的差异,MSE、MAE值越小说明拟合值与预测值之间的差异越小,模型越精确。若拟合的MSE、MAE值小,而预测的MSE、MAE值大,说明拟合值与预测值之间的差异大,存在着拟合过度的现象,模型就不精确[15]。直角双曲线模型、非直角双曲线模型、指数模型、直角双曲线修正模型应用在不同立竹密度的毛竹林下苦参时,直角双曲线修正模型两者之间的差值小,其中,在中立竹密度毛竹林下直角双曲线修正模型两者之间的差值更小一些,这可能是由于苦参幼苗在中立竹密度光照强度下生理活性更高,更有利于光合作用的进行。应用在不同立竹密度的毛竹林下决明时,均是直角双曲线修正模型两者之间差值小,直角双曲线模型差值大,并且随着立竹密度的增加直角双曲线修正模型两者之间差值越来越小,说明在弱光环境下决明幼苗光合生理活性较苦参幼苗强,直角双曲线修正模型比在强光下更为精确。研究结果也表明光响应的直角双曲线模型、非直角双曲线模型、指数模型的拟合结果与预测结果存在较大差异,存在着拟合过度的现象[16]。
光响应曲线是研究植物光合作用的主要内容之一,通过光响应曲线可以计算出最大净光合速率(Pnmax)、暗呼吸速率(Rd)、光补偿点(LCP)、光饱和点(LSP)等生理参数[17]。在本研究中,苦参和决明幼苗随着毛竹林立竹密度增大,即光照强度的降低,直角双曲线修正模型拟合的生理参数Rd均呈降低趋势,苦参LCP呈现“Ⅴ”型变化,决明LCP逐渐降低,苦参LSP呈下降趋势,决明LSP呈现“Ⅴ”型变化,与实际观测值较为接近,苦参与决明幼苗随着立竹密度的增大光补偿点和光饱和点变化趋势不同可能是由于两者不同的生理特征所致,但两种幼苗的Rd、LCP参数总体上呈现下降趋势,说明弱光对植物的光响应生理参数有负面的影响[18],也说明非直角双曲线模型和直角双曲线修正模型在拟合苦参和决明光响应时比直角双曲线模型和指数模型更适合,更符合弱光环境下苦参和决明幼苗通过降低暗呼吸速率来减少呼吸消耗的碳,以及降低光补偿点和光饱和点,最大限度地利用光量子来增加碳积累的生理应对措施[19-21],这与白菜(Brassica campestris L. ssp. chinensis Makino)[22]、黄波罗(Phellodendron amurense Rupr.)[23]、金莲花(Trollius chinensis Bunge)[24]、连翘(Forsythia suspensa (Thunb.) Vahl)[25]等在弱光或遮阴环境下的光合生理变化研究结果一致。
不同立竹密度的毛竹林下苦参和决明幼苗直角双曲线模型、非直角双曲线模型、指数模型光合拟合值与实际观测值之间偏离较大,由于这3种拟合模型的函数均是没有极值的渐近线,若没有辅助方法无法直接计算出Pnmax、LSP[26-28],冬小麦(Triticum aestivum L.)、水稻(Oryza sativa L.)[29]、巨尾桉(Eucalyptus grandis×E. urophylla)[30]光合研究中这3种模型的Pnmax计算值大于实际测量值,而LSP小于实际测量值。直角双曲线模型拟合苦参和决明幼苗光响应曲线决定系数最小,因为直角双曲线模型的函数未考虑曲线的弯曲程度,通过提高初始斜率来使得拟合值更接近实测值,反而降低了模型拟合的精确性[31];直角双曲线修正模型拟合的苦参和决明光响应曲线与观测值最接近,决定系数R2在4种模型中最大,是由于直角双曲线修正模型的函数存在极值,可直接计算出Pnmax、LSP,并且能够较好的拟合植物在饱和光强之后的光抑制现象,估算出的Pnmax、LSP值最接近真实值[32-34],所以直角双曲线修正模型拟合效果最好;且随着立竹密度的增大决定系数R2值呈增大趋势,可能是因为高立竹密度毛竹林形成良好的庇荫环境,林下苦参和决明幼苗叶片受外界光强的影响较小,在林分内对光强变化响应更敏感。
-
(1) 本研究中直角双曲线模型、非直角双曲线模型、指数模型、直角双曲线修正模型拟合和预测MSE和MAE值,应用在不同立竹密度的毛竹林下苦参和决明幼苗时,均是直角双曲线修正模型较为精确。其中,直角双曲线修正模型在中立竹密度毛竹林下苦参幼苗拟合精确性更高一些,高立竹密度毛竹林下决明幼苗拟合更高一些。
(2) 苦参和决明幼苗随着毛竹林立竹密度增大,直角双曲线模型、非直角双曲线模型、直角双曲线修正模型以及指数模型中,只有直角双曲线修正模型拟合的生理参数与实际观测值较为接近,说明直角双曲线修正模型在拟合毛竹林下苦参和决明幼苗光响应时较其它模型更为精确。
(3) 在4种模型拟合苦参和决明幼苗光响应曲线时,非直角双曲线模型拟合的决定系数R2值在4种模型中最小,直角双曲线修正模型拟合的决定系数R2值最大,可直接计算出Pnmax、LSP,且能够较好地拟合植物在饱和光强之后的光抑制现象,所以直角双曲线修正模型拟合效果最好。综合得出,不同立竹密度的毛竹林下苦参和决明幼苗用直角双曲线修正模型拟合的光响应参数和光响应曲线更为精确,拟合效果更好。
毛竹林下苦参和决明幼苗光合作用光响应模型比较
Comparison of Photosynthetic Light Response Models of Sophora flavescens and Catsia tora under Phyllostachys edulis Seedlings
-
摘要:
目的 探讨苦参和决明对不同立竹密度毛竹林下光环境的适应规律, 为毛竹林下苦参和决明的复合经营提供理论参考。 方法 以毛竹林下种子播种的固氮植物苦参和决明幼苗为试验材料, 选择立地条件和经营水平一致, 立竹密度为低(1 600±200株·hm-2)、中(2 400±200株·hm-2)、高(3 200±200株·hm-2)3种试验毛竹林, 采用直角双曲线模型、非直角双曲线模型、直角双曲线修正模型和指数模型4种光合响应模型拟合。 结果 表明:在不同立竹密度的毛竹林下, 苦参和决明拟合的均方误差(MSE)、平均绝对误差(MAE)值均是直角双曲线修正模型最小, 直角双曲线模型最大, MSE、MAE预测值也是直角双曲线模型大于直角双曲线修正模型; 4种模型拟合的苦参和决明的初始量子效率(α)、最大净光合速率(Pnmax)、暗呼吸速率(Rd)、光补偿点(LCP)存在差异, 苦参和决明在不同立竹密度的毛竹林下4种模型拟合的α值均不同, Pnmax、Rd、LCP总体上是直角双曲线模型最大, 直角双曲线修正模型较小, 并且只有直角双曲线修正模型可以直接计算出光饱和点(LSP); 在一定的光强范围内, 除直角双曲线模型外, 其余3种模型拟合的苦参和决明净光合速率(Pn)随着光强的增强而增加, 但光强超过光饱和点(LSP)后, 净光合速率(Pn)随着光强的增强而降低, 且不同立竹密度的毛竹林下苦参和决明4种光响应拟合模型的决定系数R2值均是直角双曲线修正模型最大。 结论 不同立竹密度毛竹林下苦参和决明的光响应曲线用直角双曲线修正模型拟合更精确。 Abstract:Objective To Compare the photosynthetic light response physiological parameters of four fitting models and identify the adaptability of Sophora flavescens and Catsia tora, so as to provide theoretical reference for the compound management of S. flavescens and C. tora under moso bamboo (Phyllostachys edulis). Method The S. flavescens and C. tora seedlings, the nitrogen-fixing plants, were investigated under low (1 600±200 stem·hm-2) and medium (2 400±200 stem·hm-2) and high (3 200±200 stem·hm-2) density of moso bamboo with same sites condition and management level. The light response curves of S. flavescens and C. tora leaves were measured and fitted, as well as analyzed by rectangular hyperbola, non-rectangular hyperbola, modified rectangular hyperbola model and exponential model. Result The values of fitted mean-square error (MSE) and mean absolute deviation (MAE) of S. flavescens and C. tora were the smallest for the modified rectangular hyperbola model and largest for the rectangular hyperbola model. The MSE and MAE estimated by rectangular hyperbola were more than that by modified model under different stand density of moso bamboo. The light response physiological parameters of α, Pnmax and LCP were different in the four models, and both the fitted values of α of S. flavescens and C. tora were different under different bamboo stand density, and the Pnmax, Rd and LCP estimated by rectangular hyperbola were more than the measured values, and these photosynthetic parameters estimated by the modified rectangular hyperbola model was close to the measured values. At the same time, only the modified model enables directly calculating the Lsp. Except for the rectangular hyperbola model, there was a certain law of S. flavescens and C. tora, namely, the net photosynthetic rate increased with the light intensity, then decreased while exceeding the saturation point, and the determinant R2 of modified rectangular hyperbola model was the largest in the four fitted models. Conclusion The photosynthetic light response curve of S. flavescens and C. tora fitted by modified rectangular hyperbola model is more accurate than that fitted by the other models under different stand density of moso bamboo. -
表 1 不同立竹密度毛竹林下苦参和决明幼苗的株高和地径
Table 1. The height and stem basal diameter of seedling of S. flavescens and C. tora under different density of moso bamboo
植物
Plants株高Height/cm 地径Basal Diameter/mm D1 D2 D3 D1 D2 D3 苦参S. flavescens 16.49±1.40a 12.69±1.49b 12.01±1.36b 10.12±1.08a 7.16±0.75b 6.93±0.0b 决明C. tora 30.13±2.37a 22.48±2.22b 20.75±2.09b 10.33±1.13a 9.95±1.08ab 9.22±0.98b 表 2 试验毛竹林下苦参和决明幼苗4个光响应拟合模型的MSE和MAE
Table 2. The MSE and MAE of seedling of S. flavescens and C. tora under test moso bamboo estimated by four models
植物
Plants立竹密度
Bamboo density模型
Model拟合值的MSE
Fitted MSE拟合值的MAE
Fitted MAE预测值的MSE
Test MSE预测值的MAE
Test MSE苦参
S. flavescensD1 直角双曲线模型Rectangle hyperbola 0.879 0.805 0.793 0.780 非直角双曲线模型Non-rectangle hyperbola 0.007 0.066 0.014 0.111 直角双曲线修正模型Modified rectangular hyperbola Model 0.004 0.055 0.065 0.108 指数模型Exponential Model 0.006 0.059 1.005 0.980 D2 直角双曲线模型Rectangle hyperbola 1.409 0.919 0.868 0.0824 非直角双曲线模型Non-rectangle hyperbola 0.019 0.116 0.009 0.072 直角双曲线修正模型Modified rectangular hyperbola Model 0.004 0.051 0.030 0.092 指数模型Exponential Model 0.015 0.101 1.057 1.019 D3 直角双曲线模型Rectangle hyperbola 0.162 0.107 2.679 1.442 非直角双曲线模型Non-rectangle hyperbola 0.011 0.083 0.056 0.163 直角双曲线修正模型Modified rectangular hyperbola Model 0.002 0.034 0.025 0.088 指数模型Exponential Model 0.014 0.102 0.964 0.967 决明C. tora D1 直角双曲线模型Rectangle hyperbola 4.399 1.258 2.924 1.027 非直角双曲线模型Non-rectangle hyperbola 1.041 0.773 1.232 0.787 直角双曲线修正模型Modified rectangular hyperbola Model 0.217 0.313 0.243 0.336 指数模型Exponential Model 1.047 0.779 2.267 1.400 D2 直角双曲线模型Rectangle hyperbola 4.088 1.639 3.746 1.573 非直角双曲线模型Non-rectangle hyperbola 0.053 0.195 0.243 0.335 直角双曲线修正模型Non-rectangle hyperbola 0.007 0.052 0.025 0.099 指数模型Exponential Model 0.051 0.175 0.997 0.901 D3 直角双曲线模型Rectangle hyperbola 1.128 0.880 3.018 1.205 非直角双曲线模型Non-rectangle hyperbola 0.065 0.166 0.859 0.851 直角双曲线修正模型Modified rectangular hyperbola Model 0.036 0.139 0.160 0.668 指数模型Exponential Model 0.060 0.156 3.505 1.686 表 3 试验毛竹林下苦参和决明幼苗4种光响应拟合模型参数
Table 3. The light response physilogical parameters of seedling of S. flavescen and C. tora under test moso bamboo estimated by four models
植物
Plants立竹密度
Bamboo density模型Model α Pnmax Rd LCP LSP 苦参 D1 直角双曲线模型Rectangle hyperbola 0.012 10.000 0 0.003 — S. flavescens 非直角双曲线模型Non-rectangle hyperbola 0.048 5.672 0.677 14.840 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.070 4.845 0.678 10.777 1 031.197 指数模型Exponential Model 0.043 4.745 1.135 30.554 — D2 直角双曲线模型Rectangle hyperbola 0.131 10.000 3.415 40.821 — 非直角双曲线模型Non-rectangle hyperbola 0.051 5.555 0.490 9.898 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.086 5.002 0.493 6.193 866.613 指数模型Exponential Model 0.052 4.898 1.096 23.749 — D3 直角双曲线模型Rectangle hyperbola 0.080 10.000 1.825 27.965 — 非直角双曲线模型Non-rectangle hyperbola 0.043 6.627 0.347 8.125 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.067 4.113 0.367 5.753 745.913 指数模型Exponential Model 0.046 5.992 1.053 25.478 — 决明C. tora D1 直角双曲线模型Rectangle hyperbola 0.251 10.000 5.642 51.745 — 非直角双曲线模型Non-rectangle hyperbola 0.021 3.466 0.776 37.078 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.028 3.612 0.678 26.677 572.100 指数模型Exponential Model 0.034 2.691 1.306 52.912 — D2 直角双曲线模型Rectangle hyperbola 0.005 10.000 0.007 0.139 — 非直角双曲线模型Non-rectangle hyperbola 0.022 3.547 0.670 31.568 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.031 2.920 0.655 24.827 817.604 指数模型Exponential Model 0.022 2.782 1.239 74.436 — D3 直角双曲线模型Rectangle hyperbola 0.094 10.000 5.027 108.123 — 非直角双曲线模型Non-rectangle hyperbola 0.094 2.529 0.276 23.038 — 直角双曲线修正模型Modified rectangular hyperbola Model 0.019 2.464 0.300 17.414 735.658 指数模型Exponential Model 0.017 2.262 1.148 93.390 — -
[1] Méthy M. Analysis of photosynthetic activity at the leaf and canopy levels from reflectance measurements:a case study[J]. Photosynthetica, 2016, 38(4):505-512. [2] Robert E S, Mark A, John S B. Kok effect and the quantum yield of photosynthesis[J]. Plant Physiology, 1984, 75(1)95-101. doi: 10.1104/pp.75.1.95 [3] Evans J R, Jakobsen I, gren E. Photosynthetic light-response curves:2. Gradients of light absorption and photosynthetic capacity[J]. Planta, 1993, 189(2):191-200. [4] Yu Q, Zhang Y, Liu Y, et al. Simulation of the stomatal conductance of winter wheat in response to light, temperature and CO2 changes[J]. Annals of Botany, 2004, 93(4):435. doi: 10.1093/aob/mch023 [5] Ye Z P. A new model for relationship between irradiance and the rate of photosynthesis in Oryza sativa[J]. Photosynthetica, 2007, 45(4):637-640. doi: 10.1007/s11099-007-0110-5 [6] Leakey A D, Uribelarrea M, Ainsworth E A, et al. Photosynthesis, productivity, and yield of maize are not affected by open-air elevation of CO2 concentration in the absence of drought.[J]. Plant Physiology, 2006, 140(2):779-790. doi: 10.1104/pp.105.073957 [7] 高峻, 孟平, 吴斌, 等.杏-丹参林药复合系统中丹参光合和蒸腾特性的研究[J].北京林业大学学报, 2006, 28(2):64-67. doi: 10.3321/j.issn:1000-1522.2006.02.011 [8] 朱霞, 胡勇, 王晓丽, 等.几种植物生长调节剂对决明种子萌发及幼苗生长的影响[J].作物杂志, 2010, (1):46-48. doi: 10.3969/j.issn.1001-7283.2010.01.013 [9] 樊艳荣, 陈双林, 杨清平, 等.毛竹材用林林下植被群落结构对多花黄精生长的影响[J].生态学报, 2014, 34(6):1471-1480. [10] 樊艳荣, 陈双林, 林华, 等.不同林下植被干扰措施对毛竹林下植物种群分布格局的影响[J].生物多样性, 2013, 21(6):709-714. [11] 刘广路, 范少辉, 蔡春菊, 等.不同混交模式毛竹林下土壤抗侵蚀性研究[J].水土保持通报, 2015, 35(4):12-17. [12] 樊艳荣.毛竹林下多花黄精种群生长特征及影响因子研究[D].北京: 中国林业科学研究院, 2013. [13] 蒙振斌.毛竹林下施行九节茶种植可行性研究[J].广西林业, 2008, (6):31-32. doi: 10.3969/j.issn.1004-0390.2008.06.025 [14] 魏新雨.毛竹林下仿野生套种草珊瑚技术[J].农村百事通, 2011, (21):35-38. [15] 陈卫英, 陈真勇, 罗辅燕, 等.光响应曲线的指数改进模型与常用模型比较[J].植物生态学报, 2012, 36(12):1277-1285. [16] Chen Z Y, Peng Z S, Yang J, et al. A mathematical model for describing light-response curves in Nicotiana tabacum L[J]. Photosynthetica, 2011, 49(3):467-471. doi: 10.1007/s11099-011-0056-5 [17] 蒋冬月, 钱永强, 刘俊祥, 等.基于光合-光响应特性的柳树优良无性系光能利用效率的评价[J].北京林业大学学报, 2015, 37(5):49-61. [18] Ferree D C, Mcartney S J, Scurlock D M. Influence of light on fruit set of French Hybrid Grapes[J]. Horticultural Science, 1998, 33(3):510-511. [19] Balibrea M E, Dell'Amico J, Bolarín M C, et al. Carbon partitioning and sucrose metabolism in tomato plants growing under salinity[J]. Physiologia Plantarum, 2000, 110(4):503-511. doi: 10.1111/ppl.2000.110.issue-4 [20] Pearcy R W, Sims D A. Photosynthetic acclimation to changing light environments: scaling from the leaf to the whole plant[M]//Caldwell M M, Pearcy R W. Exploitation of environmental heterogeneity by plants: ecophysiological processes above-and belowground. San Diego: Academic Press, 1994: 145-174. [21] 孟浩, 王丽萍, 王鑫, 等.辣椒耐低温弱光的研究进展[J].北方园艺, 2007, (5):55-57. doi: 10.3969/j.issn.1001-0009.2007.05.021 [22] 黄俊, 郭世荣, 吴震, 等.弱光对不结球白菜光合特性与叶绿体超微结构的影响[J].应用生态学报, 2007, 18(2):352-358. doi: 10.3321/j.issn:1001-9332.2007.02.020 [23] 王凯, 朱教君, 于立忠, 等.遮阴对黄波罗幼苗的光合特性及光能利用效率的影响[J].植物生态学报, 2009, 33(5):1003-1012. doi: 10.3773/j.issn.1005-264x.2009.05.020 [24] 吕晋慧, 王玄, 冯雁梦, 等.遮荫对金莲花光合特性和叶片解剖特征的影响[J].生态学报, 2012, 32(19):6033-6043. [25] 王建华, 任士福, 史宝胜, 等.遮荫对连翘光合特性和叶绿素荧光参数的影响[J].生态学报, 2011, 31(7):1811-1817. [26] Richardson A D, Berlyn G P. Changes in foliar spectral reflectance and chlorophyll fluorescence of four temperate species following branch cutting[J]. Tree Physiology, 2002, 22(7):499-506. doi: 10.1093/treephys/22.7.499 [27] 黄红英, 窦新永, 孙蓓育, 等.两种不同生态型麻疯树夏季光合特性的比较[J].生态学报, 2009, 29(6):2861-2867. doi: 10.3321/j.issn:1000-0933.2009.06.012 [28] 段爱国, 张建国.光合作用光响应曲线模型选择及低光强属性界定[J].林业科学研究, 2009, 22(6):765-771. doi: 10.3321/j.issn:1001-1498.2009.06.003 [29] 叶子飘, 李进省.光合作用对光响应的直角双曲线修正模型和非直角双曲线模型的对比研究[J].井冈山大学学报:自然科学版, 2010, 31(3):38-44. [30] 钱莲文, 张新时, 杨智杰, 等.几种光合作用光响应典型模型的比较研究[J].植物科学学报, 2009, 27(2):197-203. doi: 10.3969/j.issn.2095-0837.2009.02.013 [31] 陆佩玲, 于强, 罗毅, 等.冬小麦光合作用的光响应曲线的拟合[J].中国农业气象, 2001, 22(2):12-14. doi: 10.3969/j.issn.1000-6362.2001.02.003 [32] 叶子飘.光响应模型在超级杂交稻组合——Ⅱ优明86中的应用[J].生态学杂志, 2007, 26(8):1323-1326. [33] 叶子飘, 于强.光合作用光响应模型的比较[J].植物生态学报, 2008, 32(6):1356-1361. doi: 10.3773/j.issn.1005-264x.2008.06.016 [34] 叶子飘.光合作用对光和CO2响应模型的研究进展[J].植物生态学报, 2010, 34(6):727-740. doi: 10.3773/j.issn.1005-264x.2010.06.012 -



 下载:
下载: