-
森林是陆地生态系统的重要组成部分,碳储量对森林的固碳能力有重要影响[1-2]。随着全球气候变暖,森林生态系统对气候的影响成为了焦点,森林地上碳储量的相关研究不断扩展,广度和深度逐渐提高[3-4]。无论是在区域小尺度还是大尺度上,估测过程中都有着极大的不确定性。因此,如何减少这些不确定性,提高碳储量的估测精度成了研究的重点。
不确定性作为自然界中普遍存在的一种现象,包括不准确、模糊、不明确等。而碳储量计算过程中主要涉及3种不确定性:模型不确定性、测量不确定性、抽样不确定性[5-7]。Shettles等[8]将模型不确定性作为最大的误差源,约占总不确定性的70%。模型的不确定性来源主要包括变量的不确定性、残差变异、参数误差等。Michie等[9]估算生物量时计算了异速生长模型引起的误差。产生误差的主要原因是缺乏模型验证数据、样本数量不足、树种与特定异速生长模型不匹配。测量不确定性主要受测量条件、技术、设备和人为因素的影响[10-11]。抽样不确定性主要受样地大小、样本量、抽样方法和自然条件的影响。秦立厚[10]研究分析了浙江省森林生物量估算中模型的不确定性。傅煜[11]采用系统抽样的方法估测了江西省杉木生物量,通过蒙特卡洛法反复模拟单木生物量模型的过程,估测出江西省杉木地上总生物量及不确定性。因此,如何计算这些不确定性以提高森林碳储量估测的精度成为主要挑战。
传统上,森林资源调查数据是通过实地调查获得,耗时费力,并且调查结果存在很大误差。遥感技术具有快速、准确、对森林无损的优点,能够对森林进行连续的宏观监测[12]。目前在碳储量估测的研究中,Landsat8-OLI数据具有覆盖范围广、分辨率适中、免费下载等优点[13]。遥感数据能够对树冠的光谱反射率进行记录,可用于研究森林中植被的光合吸收,这与研究碳储量存在相关性。张加龙[14]等使用Landsat8-OLI影像结合梯度提升决策树模型估测出香格里拉高山松的地上生物量。采用遥感数据估测碳储量,仍然存在因子选取、建模方法、数据饱和等不确定性问题[14-15]。由于光谱影像的空间结构和纹理信息存在一定的局限性,在遥感影像分析中无法消除同物异谱、同谱异物的现象。仅基于光谱信息估测森林碳储量具有极高的不确定性。纹理特征考虑像素之间的空间关系,可以表示图像中的灰度变化,提高空间信息的识别程度[16]。研究结果表明,添加纹理特征可以有效提高模型的精度,因此考虑纹理特征对研究模型不确定性的影响具有实际意义[17]。本研究将传统的模型分析方法和蒙特卡洛模拟方法相结合,使用随机森林进行建模预测,用蒙特卡洛进行不确定性计算,反复采用随机森林联立蒙特卡洛(Random forest-Monte Carlo,RF-MC)对模型进行估测及不确定性计算,直至模型精度及不确定性趋于稳定达到最优;计算区域尺度的碳储量,并为不确定性提供稳定可靠的测定,将不确定性分为变量误差和模型误差引起的不确定性;结合蒙特卡洛和模型分析的双重优点,减少模型误差对碳储量估算的不确定性;为确定估测结果精度是否满足要求,采用相对均方根误差(rRMSE)用于量化和分析不确定性。
本研究以高山松为研究对象,采用Landsat8-OLI影像、DEM和样地数据。基于Landsat8-OLI影像提取单波段因子、比值植被指数、纹理因子、信息增强因子、地形因子、植被生长因子等变量。使用随机森林算法建立高山松地上碳储量估测模型,结合蒙特卡洛模拟分析不同变量组合对碳储量估测及不确定性的影响。
-
研究区位于云南省迪庆州香格里拉市,99°20′~100°19′ E、26°52′~28°52′ N,总面积为11 613 km2。地形起伏大,海拔高差达到4 042 m,森林覆盖率达74.99%,森林资源丰富。主要优势树种为云杉( Picea asperata Mast.) 、云南松( Pinus yunnanensis Franch.) 、高山松( Pinus densata Mast.) 、高山栎( Quercus semicarpifolia Smith.)等[18]。高山松是香格里拉市的优势树种之一,占全市面积的16.18%。纯林主要分布在2 600~3 500 m海拔的向阳山坡和河流两岸。
-
使用USGS下载的Landsat8-OLI影像数据,选取3景2015年云量较少的影像,具体信息如表1所示。影像使用ENVI5.3软件进行预处理。通过辐射定标、大气校正,消除地形和气溶胶对地物反射的影响。最后使用坡度匹配法进行地形校正,两次校正后,北坡和南坡的地形阴影平均值接近,阴坡部分的反射率得到阳坡部分反射率的值补偿。
表 1 研究区影像
Table 1. Images of the study area
调查年
Survey
yearID 获取时间
Acquisition
time云量
Cloud cover/
%
2015LC1310412015354LGN00 2015-12-20 1.53 LC1320402015313LGN00 2015-11-09 1.24 LC1320412015313LGN00 2015-11-09 0.54 -
研究区共60个样地,样地调查时间为2015年11月至2016年3月。样地大小为30 m × 30 m,每块样地间隔3 km以上。详细记录了森林树种、胸径(DBH)、树高、样地中心坐标、海拔、坡度、坡位等属性[19]。使用二元材积表计算每个样地中林木的蓄积量。
-
(1)高山松单株生物量模型[20]如下:
$ \begin{array}{c}W=0.073\times {D}^{1.739}\times {H}^{0.880}\end{array} $
(1) 其中,W为单株生物量,D为胸径,H为树高。
(2)高山松的碳储量计算公式为:
$ \begin{array}{c}{C}_{t}=W\times {f}_{c} \end{array} $
(2) Ct为高山松碳储量,fc为含碳系数,含碳系数0.513 1[21]。外业调查数据见表2。
表 2 外业调查数据
Table 2. Field survey data
指标
Index平均胸径
Mean DBH/
cm平均树高
Mean height/
m地上碳储量
Aboveground
carbon storage/
(t·hm−2)最大值 Max 22.76 14.18 87.10 最小值 Min 6.85 4.48 6.65 平均值 Mean 14.80 8.70 29.61 标准差 SD 3.68 2.11 16.33 -
以碳储量为因变量,遥感影像因子为自变量。根据各变量与碳储量的相关性选择最优因子,构建基于遥感特征因子的碳储量估测模型。为研究纹理特征对碳储量估测的影响,设置像元大小为5 × 5、9 × 9的窗口,以提高模型的性能[18,22]。
为了提高模型的精度,本研究提取的遥感因子主要包括7个单波段因子、5个植被指数、8个波段组合因子、3个信息增强因子、9个纹理因子、3个地形因子、1个植被生长因子。具体变量信息如表3所示。
表 3 变量信息
Table 3. Variable information
因子类型
Facter type因子信息
Factor information单波段因子 Single band factor C、B1、B2、B3、B4、B5、B7 植被指数 Vegetation index NDVI、DVI、ND32、ND53、ND57 简单比值指数因子 Simple ratio index factor B4/B3、B4/B2、B5/B3、B5/B4、B5/B7、B7/B3、B3/Albedo、B4*B3/B7 信息增强因子 Information enhancement factor Albedo、VIS123、MID57 纹理因子 Teture factor 均值(ME)、方差(VA)、均一性(HO)、对比度(CO)、
相关性(CR)、相异性(DI)、角二矩(SM)、熵(EN)、偏度(SK)地形因子 Topographical factor 海拔、坡度、坡向 植被生长因子 Vegetation growth factor VFC 注:表中C为海岸波段,B1、B2、B3、B4、B5、B7分别代表波段1、波段2、波段3、波段4、波段5、波段7;植被生长因子的计算公式: $VFC=(NDVI-{NDVI}_{{\rm{min}}})/({NDVI}_{{\rm{max}}}-{NDVI}_{{\rm{min}}})$其中,NDVImax与NDVImin分别为同一像素某一时间序列中的NDVI最大值与最小值。 -
随机森林(RF)是一种基于决策树的机器学习方法,其特点是采用带替换的随机抽样方法从样本数据中提取一组n个数据作为训练集,根据这些数据构建分类回归树。RF是目前最有效的非参数回归模型之一。与参数回归方法相比,该算法不需要检验变量的正态性和独立性等假设。在一定程度上可以避免过拟合现象的出现,对异常值的处理效果较好,可处理高维度数据[23]。能够评估各个特征在模型中的重要性。节点的分裂属性通常用基尼系数(Gini)或信息熵来评估,基尼系数可用于计算RF回归中每个模型特征因子的重要性。将变量重要性评分用V来表示,假设有m个特征x1, x2, x3, ···, xc,现在要计算出每个特征xj的Gini指数评分VjGini,亦即第j个特征在RF所有决策树中节点分裂不纯度的平均改变量。计算公式为:
$ \begin{array}{c}{Gini}_{m}=\displaystyle\sum\limits_{k=1}^{\left|k\right|}\displaystyle\sum\limits_{{k}^{\text{'}}\ne k}^{m}{P}_{mk}{P}_{m{k}^{\text{'}}}=1-\displaystyle\sum\limits_{k=1}^{\left|k\right|}{P}_{mk}^{2} \end{array} $
(3) 其中k为类别数,Pmk是k在m个节点中的占比。
特征xj在节点m的重要性,即节点m分支前后的Gini指数变化量如下:
$ \begin{array}{c}{V}_{jm}^{Gini}=\displaystyle\sum\limits_{i=1}^{n}{V}_{ij}^{Gini},\left({V}_{jm}^{Gini}={Gini}_{m} - {Gini}_{L} - {Gini}_{R}\right) \end{array} $
(4) GiniL和GiniR分别表示第m个节点前后的Gini指数。每个特征的重要性可以通过对所有特征的基尼指数进行归一化来获得。
-
蒙特卡洛模拟(MC)的基本思想是反复模拟一个随机事件的发生,并根据随机事件发生的频率估计其概率特征。由于区域尺度碳储量估测模型中的不确定性来源复杂且难以测量,因此MC方法在解决这个问题方面具有显著优势。反复模拟碳储量模型的建立和估测,得到碳储量估测值和误差的概率分布[24-25]。碳储量估测值的误差用均方根误差(RMSE)和相对均方根误差(rRMSE)表示。具体方法如下:
(1)使用遥感模型对所有样地的碳储量进行无偏估计
$ {\widehat{g}}_{i} $ 。(2)假设残差服从
$ {\epsilon }~\mathrm{N}\left(0,{\sigma }^{2}\right) $ 的正态分布,采用一个符合$ \epsilon \beta~\mathrm{N}\left(0,{\sigma ̂}^{2}\right) $ 的随机生成的数组来模拟新的残值$ \epsilon \beta $ ,其中$ {\sigma ̂}^{2} $ 是碳储量$ {\widehat{g}}_{i} $ 的方差。(3)将碳储量的估测值
$ {\widehat{g}}_{i} $ 与新的残差$ \epsilon \beta $ 相结合,得到了新样地碳储量$ {g}'_{i} $ 。计算方差$ Var\left({g}'_{i}\right) $ 的公式为:$ \begin{array}{c}Var\left({g}'_{i}\right)=\dfrac{{\left({\displaystyle\sum }_{i=1}^{n}{g}'_{i}-{g}_{i}\right)}^{2}}{n} \end{array} $
(5) 式(5)中,n为样地数。
(4)重复第2步和第3步,直到
$ Var\left({g}'_{i}\right) $ 趋于稳定,并且在m次模拟后,计算每个样地的碳储量均值μ、均方根误差RMSE和相对均方根误差rRMSE;计算公式为:$ \begin{array}{c}\mu =\frac{1}{m}\displaystyle\sum\limits_{x=1}^{m}{\left({g}'_{i}\right)}_{x} \end{array} $
(6) $ \begin{array}{c}RMSE=\sqrt{Var\left({g}'_{i}\right)} \end{array} $
(7) $ \begin{array}{c}rRMSE=\sqrt{Var\left({g}'_{i}\right)}/\mu \cdot 100{\text{%}} \end{array} $
(8) -
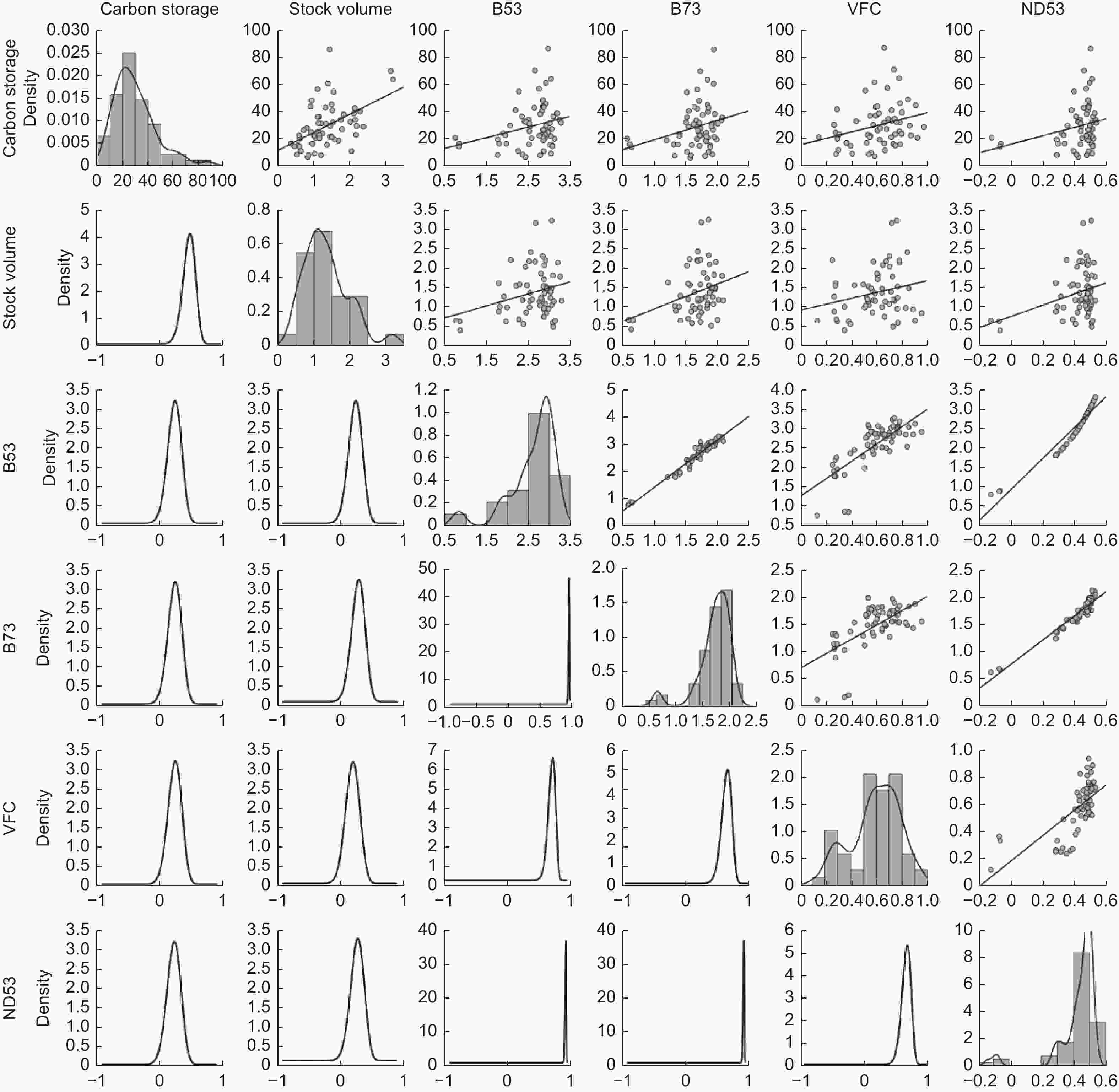
由于波段反射率、植被指数、样地数据与碳储量之间具有较高的相关性,因此根据各样地碳储量的差异,选取Stock volume、B53、B73、VFC、ND53进行相关性分析。所选特征因子之间的相关性如图1所示。右上角的图为成对特征散点图,沿对角线分布的为密度直方图,左下角为成对特征的核密度图。密度直方图显示了碳储量和蓄积量之间的正相关关系,核密度图和散点图显示出碳储量与蓄积量的相关性较强,因此把蓄积量作为建模因子。根据贝叶斯相关矩阵图可以看出5个特征因子与碳储量的相关性较强,表明波段反射率、植被指数、样地数据与碳储量的相关性较强,所以选取Stock volume、B53、B73、VFC、ND53 等5个因子构建碳储量模型。
-
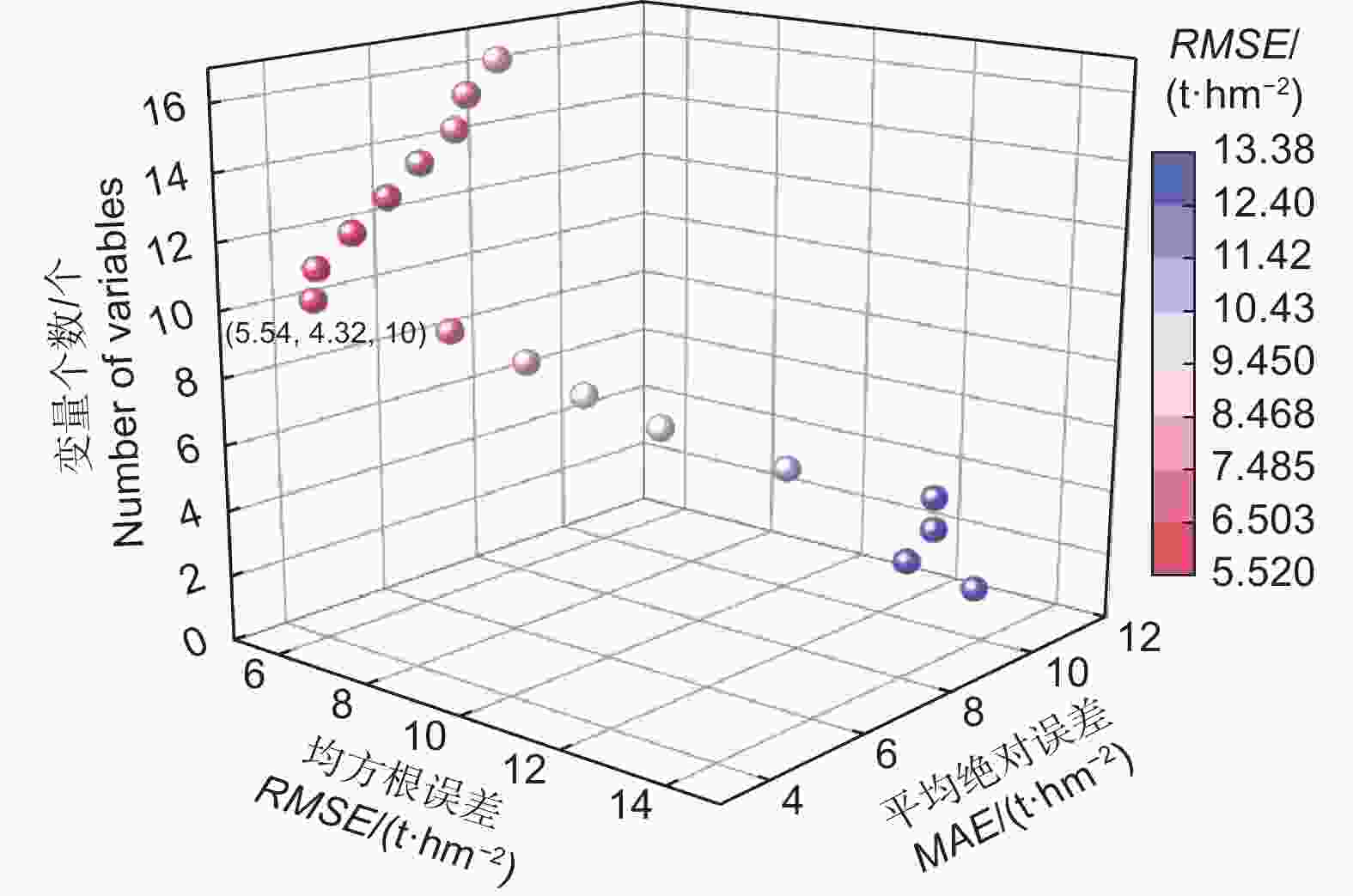
计算所选多光谱特征的各种属性,包括单波段光谱数据的均值、变异系数、标准差、方差、植被指数、波段比值、DEM数据、样地数据和基于GLCM的纹理特征。通过RFE去除具有高相关性的变量后[26],共保留了17个自变量。模型精度不一定会随着自变量数量的增加而增加,建模中包含过多的变量因素反而会增加模型的复杂度;因此,应剔除对模型精度没有显著贡献或降低模型精度的某些变量。只选择有代表性的变量进行建模。当使用10个因子建模(VFC、蓄积量、B53、B73、ND53、坡向、R9B4CR、R9B5VA、R5B3SM、R5B3SK)时,模型达到最佳精度(RMSE=5.539 t·hm−2,MAE=4.319 t·hm−2)。所有潜在变量的个数与模型精度的关系如图2所示。
-
本研究中的模型是使用RF方法构建的。为量化不同类型变量对模型的拟合度和不确定性的影响,选取10个自变量,根据属性类型组合成4种不同的方案。模型1选择VFC、蓄积量、B53、B73、ND53进行建模;模型2选择坡向、VFC、蓄积量、B53、B73、ND53进行建模;模型3选择VFC、蓄积量、B53、B73、ND53、R9B4CR、R9B5VA、R5B3SM、R5B3SK进行建模;模型4选择坡向、VFC、蓄积量、B53、B73、ND53、R9B4CR、R9B5VA、R5B3SM、R5B3SK进行建模。最后,用MC来计算每个模型的不确定性。结果如表4所示。
表 4 不同回归模型精度对比
Table 4. Comparison of accuracy of different regression models
变量 Variable R² RMSE/(t·hm−2) MAE/(t·hm−2) rRMSE/% 光谱和样地数据 Spectral and sample plots data 0.549 11.289 8.552 38.13 光谱和样地数据 + DEM Spectral and sample plots data + DEM 0.670 9.465 7.698 31.97 光谱和样地数据 + 纹理特征 Spectral and sample plots data + texture features 0.825 7.036 5.666 23.76 光谱和样地数据 + DEM + 纹理特征 Spectral and sample plots data + DEM + texture features 0.892 5.539 4.319 18.70 结果显示,基于光谱和样地数据的RF-MC模型精度最低,R2为0.549,RMSE为11.289 t·hm−2,MAE为8.552 t·hm−2。分别引入DEM和纹理特征后,模型精度有所提高。其中引入纹理特征的模型精度提高较大,说明纹理特征可以有效提升模型精度。同时引入DEM和纹理特征的RF-MC模型精度最优,R2为0.892,RMSE为5.539 t·hm−2,MAE为4.319 t·hm−2。该模型比其他相关研究的拟合程度高,如温小荣等人对建德市杉木生物量的估测R2仅为0.8[27]。
-
由表4可知,模型的不确定性随R²的增大而降低,模型的残差变异会影响预测结果,从而影响预测值的方差。因此残差值的增大会导致模型R²降低,模型的预测结果受到限制,不确定性随之增加。4种模型的不确定性随着DEM和纹理特征的引入逐渐降低,rRMSE分别为38.13%,31.97%,23.76%,18.70%。随着DEM和纹理信息的同时引入,原本仅基于光谱和样地数据模型的不确定性减少了19.43%,说明DEM和纹理特征对降低高山松地上碳储量反演模型的不确定性有一定作用。
-
4种模型中不同变量的重要性如图3所示。
Gini指数用于计算RF回归中每个模型特征的重要性。每个因子对模型的重要性如图3所示,第1、2种模型中蓄积量占比最多;添加纹理特征后,模型3和模型4中纹理因子的贡献率超过蓄积量,但蓄积量仍然在各模型中占比很大,说明把蓄积量引入作为建模因子有很大的发展潜力。纹理特征作为建模贡献率最高的因子可有效提高模型的精度。
-
为了量化不同类型变量对模型精度的影响,本研究将变量组合成4种模型,分别进行建模和预测。预测结果的散点图如图4所示。
根据图4,模型精度与拟合度呈正相关。基于光谱和样地数据的RF-MC模型,模型拟合度R2为0.549,逐步引入DEM数据和GLCM纹理特征后,R2最终增加到0.892。随着不同类型变量的引入,R²逐渐增大,模型的不确定性得到有效降低。表明RF-MC方法在估测地上碳储量方面效果显著,建模因子的选择对模型的精度及不确定性有显著影响。
-
遥感影像提取的数据只能提供森林水平方向的光谱信息。胸径和树高两个因子反映树木的垂直结构。这些因子与碳储量估测密切相关,减少数据饱和问题[28]。Wang[29]使用iPad Pro LiDAR传感器成功估算了树木的DBH。Duan[30]使用机载LiDAR和DEM数据基于树冠分割和地形偏差引起的修正方法提取树高。本研究中,引入蓄积量作为建模因子来提供森林的垂直结构信息,不受数据饱和度的影响,贡献率高(图3)。因此,采用水平和垂直值相结合的方式获取森林结构数据,以提高植被复杂地区的预测能力。如Sinha[31]利用光学和合成孔径雷达(SAR)数据成功估测印度热带落叶林的碳储量。
相关研究表明温度、二氧化碳浓度和降水对碳储量估测具有复杂的影响。单独升高温度会增强植物蒸腾作用,导致光合作用受到抑制和碳储量减少。上述3个因素的综合作用显著改善植物的生长[32-33]。气候变化通过改变树木物候和生长季节长度对树木的生长产生影响[34]。气候因子被认为是一个气候周期的平均值,在时间上与碳储量估测数据不同步。而提高建模精度的关键是解决气候因子和碳储量估测数据的同步问题。地形和气候因素对植物地上生长的影响较大,不同地理特征和气候条件的地区反演碳储量需根据实际情况适当地选择和设置可变因素和模型参数。
研究表明,高分辨率数据能够提供丰富的纹理信息,添加纹理信息可有效提高碳储量预测模型的精度[35]。由于高分辨率数据并未完全覆盖研究区,则选择空间分辨率为30 m的Landsat8-OLI遥感影像数据,该数据估测碳储量模型拟合度R2=0.892。综上所述,具有丰富纹理信息的高分辨率数据在碳储量估测中的应用有待进一步探索。
研究使用RF-MC方法的优势在于,可以对碳储量的不确定性进行稳定估测[36]。传统的模型分析方法被引入MC,经多次模拟,模型参数及其协方差矩阵的可变性逐渐减小[37],降低估测结果的残差水平。随着模拟次数增加,碳储量估测值的不确定性趋于稳定[38]。傅煜的研究结果表明,蒙特卡洛的不确定性值达到平稳状态的运算时间随建模样本量的增大而减少[11]。McRoberts[39]在美国明尼苏达州东北部设立研究区并采用蒙特卡洛方法分析了模型预测单木材积的不确定性,并指出利用模型计算大面积森林蓄积量引起的不确定性较小。改进MC方法是对输入参数进行有效抽样,减少输入参数组合的数量,以提高计算效率,如增大计算区域,样本量增加能提高估测精度降低不确定性,MC结果达到稳定所需要的运算时间逐渐缩短,可以在一定程度上提高工作效率。MC可以有效降低模型的不确定性,为研究碳储量和类似应用提供了显著优势[40]。碳储量预测值在上下端波动较大,中间较小,目前的技术和设备无法完全消除碳储量预测中的数据饱和度问题[41-42]。为降低饱和度对碳储量预测的影响,可以增加信息量更大的纹理特征、垂直结构信息、气候因子等不受数据饱和度影响的指标,有助于提高碳储量估测的精度,获得更好的预测结果。
-
本研究以高山松为研究对象,采用Landsat8-OLI遥感影像数据、DEM和样地数据,建立不同特征组合的RF回归模型,同时使用MC方法计算每个模型的不确定性。得出以下结论:①引入地形因子碳储量估测模型的精度得到提升,R2提高0.121、RMSE降低1.824 t·hm−2、MAE降低0.854 t·hm−2,不确定性降低6.16%。②纹理特征在原始图像亮度的基础上增强了空间信息的识别程度,可以显著提高森林地上碳储量的估测精度。③合理选择建模变量可以提高模型的精度,降低模型的不确定性。④RF-MC方法可以为区域尺度上的碳储量估测及其不确定性分析提供稳定可靠的结果。
基于随机森林和蒙特卡洛的高山松地上碳储量估测及不确定性分析
Estimation and Uncertainty Analysis of Aboveground Carbon Storage of Pinus densata based on Random Forests and Monte Carlo
-
摘要:
目的 为了解决碳储量的不确定性受单一类型变量的影响,而忽略了残差变异导致模型不确定性的问题,研究不同类型变量对碳储量估测模型的不确定性。 方法 以香格里拉市高山松为研究对象,采用随机森林联立蒙特卡洛(RF-MC),基于不同变量组合建立回归模型,判断各模型的不确定性。 结果 表明:(1)光谱和样地数据直接参与RF-MC模型的估测精度及不确定性最差。(2)在上一步的基础上引入纹理特征的模型预测结果优于引入DEM。(3)同时引入DEM和纹理特征的RF-MC模型效果最优(R2=0.892,RMSE=5.539 t·hm−2,MAE = 4.319 t·hm−2, rRMSE=18.7%)。模型拟合度提高了0.343,模型的不确定性降低了19.43%。 结论 基于多特征的RF-MC方法在碳储量估测中效果较好,不同类型的变量对碳储量估测精度及不确定性有一定的影响。 Abstract:Objective To study the model uncertainty induced by different types of variables on carbon storage estimation. Method Taking as the research object, Random forest joint Monte Carlo (RF-MC) was used to establish a carbon storage regression model of Shangri-La Pinus densata based on different variable combinations to determine the uncertainty of each model. Result (1) Spectral and plot data directly contributed to the estimation accuracy and uncertainty of the RF-MC model. (2) The model prediction introducing texture features was better than introducing DEM. (3) The RF-MC model that introduced both DEM and texture features performed the best (R2=0.892, RMSE=5.539 t·hm−², MAE = 4.319 t·hm−², rRMSE=18.7%). The model fit improved by 0.343 and the uncertainty of the model decreased by 19.43%. Conclusion The RF-MC method based on multiple characteristics performs well on carbon storage estimation. Different types of variables have certain impact on the accuracy and uncertainty of carbon storage estimation. -
Key words:
- carbon storage
- / random forest
- / Monte Carlo simulation
- / uncertainty
-
表 1 研究区影像
Table 1. Images of the study area
调查年
Survey
yearID 获取时间
Acquisition
time云量
Cloud cover/
%
2015LC1310412015354LGN00 2015-12-20 1.53 LC1320402015313LGN00 2015-11-09 1.24 LC1320412015313LGN00 2015-11-09 0.54 表 2 外业调查数据
Table 2. Field survey data
指标
Index平均胸径
Mean DBH/
cm平均树高
Mean height/
m地上碳储量
Aboveground
carbon storage/
(t·hm−2)最大值 Max 22.76 14.18 87.10 最小值 Min 6.85 4.48 6.65 平均值 Mean 14.80 8.70 29.61 标准差 SD 3.68 2.11 16.33 表 3 变量信息
Table 3. Variable information
因子类型
Facter type因子信息
Factor information单波段因子 Single band factor C、B1、B2、B3、B4、B5、B7 植被指数 Vegetation index NDVI、DVI、ND32、ND53、ND57 简单比值指数因子 Simple ratio index factor B4/B3、B4/B2、B5/B3、B5/B4、B5/B7、B7/B3、B3/Albedo、B4*B3/B7 信息增强因子 Information enhancement factor Albedo、VIS123、MID57 纹理因子 Teture factor 均值(ME)、方差(VA)、均一性(HO)、对比度(CO)、
相关性(CR)、相异性(DI)、角二矩(SM)、熵(EN)、偏度(SK)地形因子 Topographical factor 海拔、坡度、坡向 植被生长因子 Vegetation growth factor VFC 注:表中C为海岸波段,B1、B2、B3、B4、B5、B7分别代表波段1、波段2、波段3、波段4、波段5、波段7;植被生长因子的计算公式: $VFC=(NDVI-{NDVI}_{{\rm{min}}})/({NDVI}_{{\rm{max}}}-{NDVI}_{{\rm{min}}})$其中,NDVImax与NDVImin分别为同一像素某一时间序列中的NDVI最大值与最小值。 表 4 不同回归模型精度对比
Table 4. Comparison of accuracy of different regression models
变量 Variable R² RMSE/(t·hm−2) MAE/(t·hm−2) rRMSE/% 光谱和样地数据 Spectral and sample plots data 0.549 11.289 8.552 38.13 光谱和样地数据 + DEM Spectral and sample plots data + DEM 0.670 9.465 7.698 31.97 光谱和样地数据 + 纹理特征 Spectral and sample plots data + texture features 0.825 7.036 5.666 23.76 光谱和样地数据 + DEM + 纹理特征 Spectral and sample plots data + DEM + texture features 0.892 5.539 4.319 18.70 -
[1] 周玉荣, 于振良, 赵士洞. 我国主要森林生态系统碳贮量和碳平衡[J]. 植物生态学报, 2000, 24(5):518-522. [2] Myneni R B, Dong J, Tucker C J,et al. A large carbon sink in the woody biomass of Northern forests[J]. Proceedings of the National Academy of Sciences, 2001, 98(26): 14784-14789. doi: 10.1073/pnas.261555198 [3] Güner Ş T, Çömez A, Özkan K. Predicting soil and forest floor carbon stocks in Western Anatolian Scots pine stands, Turkey[J]. African Journal of Agricultural Research, 2012, 7(28): 4075-4083. [4] Schlamadinger B, Bird N, Johns T,et al. A synopsis of land use, land-use change and forestry (LULUCF) under the Kyoto Protocol and Marrakech Accords[J]. Environmental Science & Policy, 2007, 10(4): 271-282. [5] 秦立厚. 浙江省森林碳储量估算不确定性研究[D]. 临安: 浙江农林大学, 2017. [6] 黄屹杰, 张加龙, 胡耀鹏, 等. 高山松地上生物量遥感估算的不确定性分析[J]. 浙江农林大学学报, 2022, 39(3):531-539. [7] Gertner G Z. The sensitivity of measurement error in stand volume estimation[J]. Canadian Journal of Forest Research, 1990, 20(6): 800-804. doi: 10.1139/x90-105 [8] Shettles M, Hilker T, Temesgen H. Examination of uncertainty in per unit area estimates of aboveground biomass using terrestrial LiDAR and ground data[J]. Canadian Journal of Forest Research, 2016, 46(5): 706-715. doi: 10.1139/cjfr-2015-0265 [9] Breugel M V, Ransijn J, Craven D,et al. Estimating carbon stock in secondary forests: decisions and uncertainties associated with allometric biomass models[J]. Forest Ecology and Management, 2011, 262(8): 1648-1657. doi: 10.1016/j.foreco.2011.07.018 [10] 秦立厚, 张茂震, 钟世红, 等. 森林生物量估算中模型不确定性分析[J]. 生态学报, 2017, 37(23):7912-7919. [11] 傅 煜, 雷渊才, 曾伟生. 单木生物量模型估计区域尺度生物量的不确定性[J]. 生态学报, 2015, 35(23):7738-7747. [12] 刘 茜, 杨 乐, 柳钦火, 等. 森林地上生物量遥感反演方法综述[J]. 遥感学报, 2015, 19(1):62-74. [13] Cohen R, Kaino J, Okello J A,et al. Propagating uncertainty to estimates of above-ground biomass for Kenyan mangroves: A scaling procedure from tree to landscape level[J]. Forest Ecology and Management, 2013, 310: 968-982. doi: 10.1016/j.foreco.2013.09.047 [14] 张加龙, 胥 辉, 陆 驰. 应用Landsat8 OLI和GBRT对高山松地上生物量的估测[J]. 东北林业大学学报, 2018, 46(8):25-30. doi: 10.3969/j.issn.1000-5382.2018.08.005 [15] Zhao P, Lu D S, Wang G X,et al. Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation[J]. Remote Sensing, 2016, 8(6): 469. doi: 10.3390/rs8060469 [16] 郝 泷, 刘 华, 陈永富, 等. 耦合光谱、纹理信息的森林蓄积量估算研究[J]. 山地学报, 2017, 35(2):246-254. [17] Liao Z M, He B B, Quan X W. Potential of texture from SAR tomographic images for forest aboveground biomass estimation[J]. International Journal of Applied Earth Observation and Geoinformation, 2020, 88: 102049. doi: 10.1016/j.jag.2020.102049 [18] 岳彩荣. 香格里拉县森林生物量遥感估测研究[D]. 北京: 北京林业大学, 2012. [19] Zheng S, Cao C X, Dang Y F,et al. Retrieval of forest growing stock volume by two different methods using Landsat TM images[J]. International Journal of Remote Sensing, 2014, 35(1): 29-43. doi: 10.1080/01431161.2013.860567 [20] 孙雪莲. 基于Landsat8-OLI的香格里拉高山松林生物量遥感估测模型研究[D]. 昆明: 西南林业大学, 2016. [21] 王金亮, 王小花, 岳彩荣, 等. 滇西北香格里拉森林4个建群种的含碳率[J]. 生态环境学报, 2012, 21(4):613-619. [22] 张加龙, 胥 辉. 基于遥感的高山松连清固定样地地上生物量估测模型构建[J]. 北京林业大学学报, 2020, 42(7):1-11. [23] Bao R, Zhang J L, Lu C,et al. Estimating above-ground biomass of Pinus densata Mast. using best slope temporal segmentation and Landsat time series[J]. Journal of Applied Remote Sensing, 2021, 15(2): 024507. [24] Tang W B, Xu G S, Zhang S J. Dimensional variation analysis for rigid part assembly with an improvement of Monte Carlo simulation[J]. Ieee Access, 2020, 8: 5862-5872. doi: 10.1109/ACCESS.2019.2963400 [25] 傅 煜, 雷渊才, 曾伟生. 区域尺度杉木生物量估计的不确定性度量[J]. 林业科学, 2014, 50(12):79-86. [26] Zhou Q F, Zhou H, Zhou Q Q,et al. Structure damage detection based on random forest recursive feature elimination[J]. Mechanical Systems and Signal Processing, 2014, 46(1): 82-90. doi: 10.1016/j.ymssp.2013.12.013 [27] 温小荣, 孟 雪, 刘 俊, 等. 基于不同立地质量的杉木生物量遥感估测[J]. 林业科学研究, 2016, 29(4):494-499. doi: 10.3969/j.issn.1001-1498.2016.04.004 [28] Laurin G V, Ding J Q, Disney M,et al. Tree height in tropical forest as measured by different ground, proximal, and remote sensing instruments, and impacts on above ground biomass estimates[J]. International Journal of Applied Earth Observation and Geoinformation, 2019, 82: 101899. doi: 10.1016/j.jag.2019.101899 [29] Wang F Y, Heenkenda M K, FreeburnJ T. Estimating tree diameter at breast height (DBH) using an iPad Pro LiDAR sensor[J]. Remote Sensing Letters, 2022, 13(6): 568-578. doi: 10.1080/2150704X.2022.2051635 [30] Duan Z G, Zhao D, ZengY,et al. Assessing and correcting topographic effects on forest canopy height retrieval using airborne LiDAR data[J]. Sensors, 2015, 15(6): 12133-12155. doi: 10.3390/s150612133 [31] Sinha S, Mohan S, Das A K,et al. Multi-sensor approach integrating optical and multi-frequency synthetic aperture radar for carbon stock estimation over a tropical deciduous forest in India[J]. Carbon Management, 2020, 11(1): 39-55. doi: 10.1080/17583004.2019.1686931 [32] Bréda N, Brunette M. Are 40 years better than 55? An analysis of the reduction of forest rotation to cope with drought events in a Douglas fir stand[J]. Annals of Forest Science, 2019, 76(2): 1-12. [33] Girardin M P, Hogg E H, Bernier P Y,et al. Negative impacts of high temperatures on growth of black spruce forests intensify with the anticipated climate warming[J]. Global Change Biology, 2016, 22(2): 627-643. doi: 10.1111/gcb.13072 [34] Xie Y L, Lei X D, Shi J N. Impacts of climate change on biological rotation of Larix olgensis plantations for timber production and carbon storage in northeast China using the 3-PGmix model[J]. Ecological Modelling, 2020, 435: 109267. doi: 10.1016/j.ecolmodel.2020.109267 [35] Eckert S. Improved forest biomass and carbon estimations using texture measures from WorldView-2 satellite data[J]. Remote Sensing, 2012, 4(4): 810-829. doi: 10.3390/rs4040810 [36] Zhang Y, Liu J F, Wen Z Y. Predicting surface urban heat island in Meihekou city, China: A combination method of monte carlo and random forest[J]. Chinese Geographical Science, 2021, 31(4): 659-670. doi: 10.1007/s11769-021-1215-7 [37] Wu M, Feng Q, Wen X H,et al. Random forest predictive model development with uncertainty analysis capability for the estimation of evapotranspiration in an arid oasis region[J]. Hydrology Research, 2020, 51(4): 648-665. doi: 10.2166/nh.2020.012 [38] Heijungs R. On the number of Monte Carlo runs in comparative probabilistic LCA[J]. The International Journal of Life Cycle Assessment, 2020, 25(2): 394-402. doi: 10.1007/s11367-019-01698-4 [39] McRoberts R E, Westfall J A. Effects of uncertainty in model predictions of individual tree volume on large area volume estimates[J]. Forest Science, 2014, 60(1): 34-42. doi: 10.5849/forsci.12-141 [40] 赵 菡, 雷渊才, 符利勇. 江西省不同立地等级的马尾松林生物量估计和不确定性度量[J]. 林业科学, 2017, 53(8):81-93. [41] Gizachew B, Solberg S, Næsset E,et al. Mapping and estimating the total living biomass and carbon in low-biomass woodlands using Landsat 8 CDR data[J]. Carbon Balance and Management, 2016, 11(1): 1-14. doi: 10.1186/s13021-015-0043-4 [42] Vafaei S, Soosani J, Adeli K,et al. Improving accuracy estimation of forest aboveground biomass based on incorporation of ALOS-2 PALSAR-2 and Sentinel-2A imagery and machine learning: A case study of the Hyrcanian forest area (Iran)[J]. Remote Sensing, 2018, 10(2): 172. doi: 10.3390/rs10020172 -
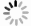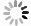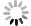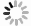



 下载:
下载: