-
树冠是树木与周围环境相互作用的重要场所，光合作用、呼吸作用、蒸腾作用等一系列与树木生长密切相关的生理活动都发生在树冠中[1]。冠长率（CR）是活冠长与树高的比值，是树冠结构的重要组成因子之一[2]，可用于评估树木健康程度、木材质量、火灾发生的风险[1,3-4]。此外，冠长率还可以间接反映树木的光合能力、竞争能力以及林木之间的相对优势地位[5-7]。冠长率常作为重要预测变量加入到林木生长模型中，以改善模型拟合效果[8-9]。然而，在野外调查时，由于林层结构复杂，冠长率往往无法精准且省时省力的测量[10-11]，因此构建冠长率模型具有重要意义。
冠长率可以表达为树木大小、竞争、立地因子的函数[12]。胸径、树高反映了树木的发育阶段，因此可以解释大部分冠长率的变异。林木竞争反映了树木获取光资源以及空间资源的能力，也是影响树木冠长率的重要因子，预测单木冠长率会因缺失竞争变量而产生高估或低估的拟合结果[13-14]。立地特征一般用坡度、坡向、坡位、海拔等生态因子表示，由于林木所处的立地条件不同，进而影响树木的生长[15]。除此之外，为研究不同林层的冠长率变化规律，Sharma等[16]以哑变量的形式将林层作为解释变量加入冠长率模型中，结果表明，林层的加入显著提升了模型拟合优度，不同林层间的冠长率具有较大差异。目前已有多个学者对冠长率模型进行构建并已取得较好结果[12,16-17]，但由于数据缺乏，探讨冠长率随不同地形因子变化规律的研究较少。地形影响林木的生长与分布[2]，研究不同地形条件下林木冠长率之间的差异，对了解林木生长规律具有重要意义。分别构建不同地形条件下的冠长率模型比较复杂且不利于应用，而使用哑变量处理分类变量的方法为模型合并提供了可能的途径[18]，目前在林业中得到了广泛应用[19-20]
红松（Pinus koraiensis Siebold and Zucc.）在辽东山区分布广泛，作为地带性顶级群落主要树种之一，有着重要的经济与生态价值[21]。然而，关于辽东山区红松人工林单木冠长率模型的研建还比较缺乏。因此，本研究基于辽宁省清原县大边沟林场64块固定样地每木检尺数据，构建了基于林木竞争、地形因子的不同林层的人工红松冠长率预估模型，选取对红松单木冠长率影响较大的地形因子，分析冠长率随林木大小、竞争、林层、地形的变化规律，为辽东山区红松人工林森林生长动态预估奠定基础。
-
研究区域位于辽宁省清原县大边沟林场（41°51′～42°00′ N，124°59′～125°18′ E）。大边沟林场在辽宁东部，属于中低山地区，海拔范围为500～700 m。夏季炎热多雨，冬季寒冷干燥，属于温带季风性气候，年降水量700～800 mm，主要集中在夏季。土壤以暗棕壤和棕壤为主，适合针阔叶树生长。森林植被由天然次生林与人工林组成，人工林占森林植被的大多数，以红松、落叶松（Larix gmelinii (Rupr.) Kuzen.）等针叶树种为主。
-
2020年6月在清原县大边沟林场选取10～55 a不同年龄段的红松人工林，共设置64块标准地，标准地面积大小为0.06 hm2（20 m × 30 m）。对标准地内的所有树木进行每木检尺，分别测量所有树木胸径、树高、冠幅、第一活枝高等林木因子，同时记录各样地坡度、坡位、坡向等地形因子，去除异常数据，共获得2 640株测量数据，按3:1的比例对2 640株红松每木检尺数据进行随机取样，1 980株用于建模，660株用于模型检验。建模和检验数据的具体信息见表1。
数据
Data变量
Variable最小值
Minimum最大值
Maximum平均值
Mean标准差
SD变异系数
CV/%建模数据 Fitting data 年龄 Age/a 10 55 28 14 50 胸径 D/cm 0.8 47.1 17.4 9.5 55 树高 H/m 1.1 29.8 10.7 5.1 48 冠长率 CR 0.23 0.96 0.68 0.16 23 检验数据 Validation data 年龄 Age/a 10 55 29 14 50 胸径 D/cm 1.2 43.0 17.8 9.2 52 树高 H/m 0.7 25.5 11.1 5.1 46 冠长率 CR 0.24 0.95 0.68 0.16 23 Table 1. Statistics of individual tree characteristics of Pinus koraiensis plantation
-
通过查阅国内外文献选出6个非线性模型形式作为冠长率候选模型，如表2所示。
编号
Number模型类型
Model type表达式
Expression formula参考文献
ReferenceCR1 逻辑斯蒂 $CR=1/(1 + {{\rm{e}}}^{-\beta X})$ [11] CR2 理查德 ${CR=a/(1 + b{ {\rm{e} } }^{-{\rm{c}}\beta X})}^{\frac{1}{m} }$ [6] CR3 理查德 ${CR=1/(1 + {{\rm{e}}}^{-\beta X})}^{\frac{1}{2} }$ [22] CR4 指数 $CR={{\rm{e}}}^{\beta X}$ [10] CR5 指数 $CR=1-{ {\rm{e} } }^{-{\rm{c}}\beta X}$ [23] CR6 威布尔 $CR=a\times (1-b{ {\rm{e} } }^{-{\rm{c}}\beta {X}^{\omega } })$ [6] 注：CR是冠长率，a、b、c、m、ω是模型参数，a、b、c均为1，m=6，ω=10。β为参数向量，X为变量向量。
Note: CR is the crown ratio, a、 b、 c、 m、ω are the model parameters, a、b、c = 1, m = 6, ω = 10. β indicates the parameter vector and X indicates the vector of variables.Table 2. Crown ratio candidate models
将对冠长率影响最大的胸径以及树高因子作为自变量，采用最小二乘法对6个模型分别进行拟合。采用调整后的决定系数（R2a）、均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）对6个模型的拟合结果进行评价与检验，选取R2a最大、RMSE、MAE、MAPE最小的作为最优基础模型。评价以及检验指标如下：
式中:yi为第i株树的冠长率实际值，
$ \widehat{{y}_{i}} $ 为第i株树的冠长率估计值，$ \overline{y} $ 为冠长率观测值的平均值，p为模型估计参数的个数，n为样本数。采用再参数化的方法将竞争指标-对象木的相对直径（Rd）代入到最优基础模型，探究竞争对于冠长率的影响，Rd的计算公式如下：
式中：Rd是对象木的相对直径，Di是第i株树的胸径，Dg是林分平均胸径。
根据实测数据将坡度按0～5°、5～15°、15～25°划分为3级，将坡向按阴坡、阳坡、半阳坡划分为3级，将坡位按上坡、中坡、下坡划分为3级，采用国际林联划分标准，将林层以林木优势高的2/3作为分界点划分为上林层与下林层。将坡度、坡位、坡向作为哑变量分别加入到模型中，依据R2a选取对冠长率模型影响最大的地形因子，在此基础上将林层作为哑变量加入到模型中，最终构建基于竞争、地形与林层的冠长率模型，以CR4模型为例将坡向、林层作为哑变量可表示为：
式中：a0，a1，b，c0，c1，c2为模型参数，D为胸径，H为树高。Fl为区分林层的哑变量，当Fl为0时代表上林层，当Fl为1时代表下林层 。Az1、Az2为区分坡向的哑变量，当Az1为1，Az2为0时代表阳坡，Az1为0，Az2为1时代表半阳坡，Az1为0，Az2为0时代表阴坡。
采用F统计指标检验引入哑变量前后模型是否有显著差异，有显著差异表明不同地形因子与林层对冠长率有影响，引入哑变量有意义，采用MSER作为评价新增变量对模型贡献的评价指标。公式如下：
式中：SSEbase和SSEdumb分别是基础模型和哑变量模型的残差平方和；dfbase和dfdumb分别是基础模型和哑变量模型的自由度，MSEi为含有林分变量的冠幅模型均方误差，MSEj为未引入林分变量的基础模型均方误差。
-
冠长率基础模型的拟合结果如表3所示，由表3可以看出，在引入胸径以及树高的情况下，6个模型中CR4的R2a均最高，RMSE均最低，效果最好，CR2次之，模型的检验指标MAE、MAPE也体现出了与之相同的结果，因此将CR4模型作为最优基础模型。通过再参数化方法引入Rd，发现将参数c进行再参数化处理时效果最好（R2a=0.402，RMSE=0.124，MESR=14.14%），与CR4模型相比拟合效果大幅度提高，说明竞争显著影响林木冠长率。经再参数化处理后的模型形式如下：
模型
Model建模数据 Fitting data 检验数据 Validation data R2a RMSE MAE MAPE/% CR1 0.241 0.139 0.113 18.97 CR2 0.282 0.135 0.110 18.47 CR3 0.253 0.138 0.112 18.83 CR4 0.302 0.134 0.108 18.22 CR5 0.213 0.142 0.116 19.39 CR6 0.259 0.138 0.112 18.77 Table 3. Fitting evaluation of crown ratio candidate models
-
在模型（10）的基础上分别将坡度、坡向、坡位作为哑变量加入到模型中。采用R2a、RMSE选取对模型贡献最大的地形因子，并采用F统计指标检验与基础模型（10）的显著性差异，加入哑变量后模型的拟合优度指标及F检验如表4所示。结果表明，将坡度作为哑变量加到参数b、将坡位、坡向加到参数c上效果均优于未加入哑变量的模型（10）。从F统计指标检验结果来看，加入哑变量后模型与模型（10）均有显著性差异。经比较，将坡向作为哑变量的模型拟合效果以及检验效果优于坡度及坡位，说明坡向是影响人工红松单木冠长率的最重要的地形因子。
引入哑变量的因子 Dummy variables 引入参数 Parameters R2a RMSE MAE MAPE/% F值 P值 MSER/% 无 — 0.402 0.124 0.099 16.83 — — 坡度 b 0.412 0.123 0.099 16.72 19.31 <0.01 坡位 c 0.412 0.122 0.099 16.83 21.69 <0.01 坡向 c 0.412 0.122 0.096 16.37 21.69 <0.01 2.25 坡向、林层 c、a 0.415 0.122 0.096 16.34 6.02 <0.01 0.16 Table 4. Fitting results of dummy variable models
为研究林层对冠长率的影响，在含有坡向冠长率模型的基础之上，进一步将林层作为哑变量引入到模型中，拟合指标如表4所示。由表4可以看出，将坡向、林层作为哑变量加到参数c、a上构建的模型显示出更好的拟合效果。F统计检验结果表明，加入林层哑变量后与未加入林层的模型差异显著（F=6.19，P<0.01），这说明林分竞争、地形与林层对模型贡献较大。最终模型参数估计值见表5，最终模型形式如下：
模型
Model指标
Index参数 Parameters a0 a1 b c0 c1 c2 d 哑变量模型 估计值 −0.093 5 −0.028 8 −0.008 1 −0.050 4 −0.006 1 −0.004 3 0.039 4 标准误 0.013 4 0.009 8 0.001 8 0.002 5 0.001 0 0.000 9 0.002 6 t值 −6.97 −2.94 −4.43 −20.38 −5.85 −4.73 14.91 p值 ＜0.01 ＜0.01 ＜0.01 ＜0.01 ＜0.01 ＜0.01 ＜0.01 Table 5. Parameter estimation results of dummy variable model
式中：a0、a1、b、c0、c1、c2、d为模型参数，D为胸径，Rd为相对直径，H为树高。Fl为区分林层的哑变量，当Fl为0时代表上林层，当Fl为1时代表下林层。Az1、Az2为区分坡向的哑变量，当Az1为0，Az2为1时代表半阳坡，当Az1为1，Az2为0时代表阳坡，Az1为0，Az2为0时代表阴坡。
-
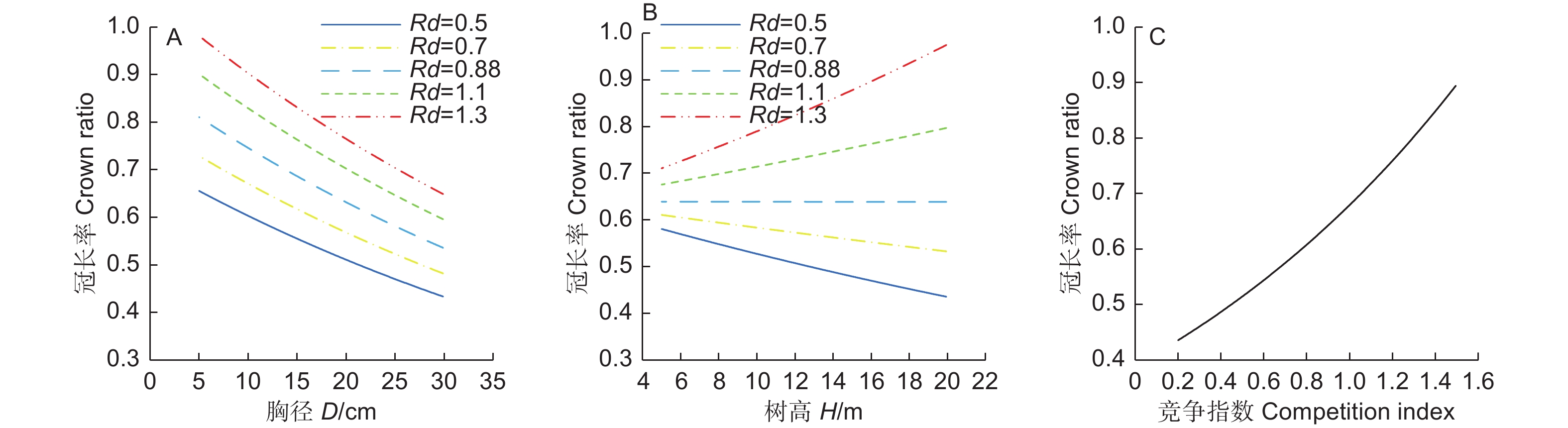
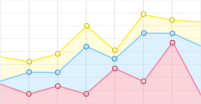
基于最终哑变量模型的参数，分别模拟了冠长率随胸径、树高、对象木竞争水平（Rd）的变化规律（图1），不同坡向及林层对冠长率的影响（图2，3）。图1A为不同Rd水平的冠长率随胸径变化曲线，由图1A可知，冠长率呈现随胸径的增大而减小的规律，且并不随着Rd的变化而改变。由图1B可知，Rd不同冠长率呈现出不同变化规律。Rd较小时，冠长率随树高增加呈现减小的趋势，随着Rd的增大，冠长率减小的趋势逐渐变缓。随Rd进一步增大，冠长率随树高增加呈现增大的趋势。冠长率随对象木竞争水平的增大而增大（图1C）。
Figure 1. Variation law of crown ratio with forest factors and competition factors
Figure 2. Comparison of crown ratio in different slope aspects
Figure 3. Comparison of crown ratio in different forest layers
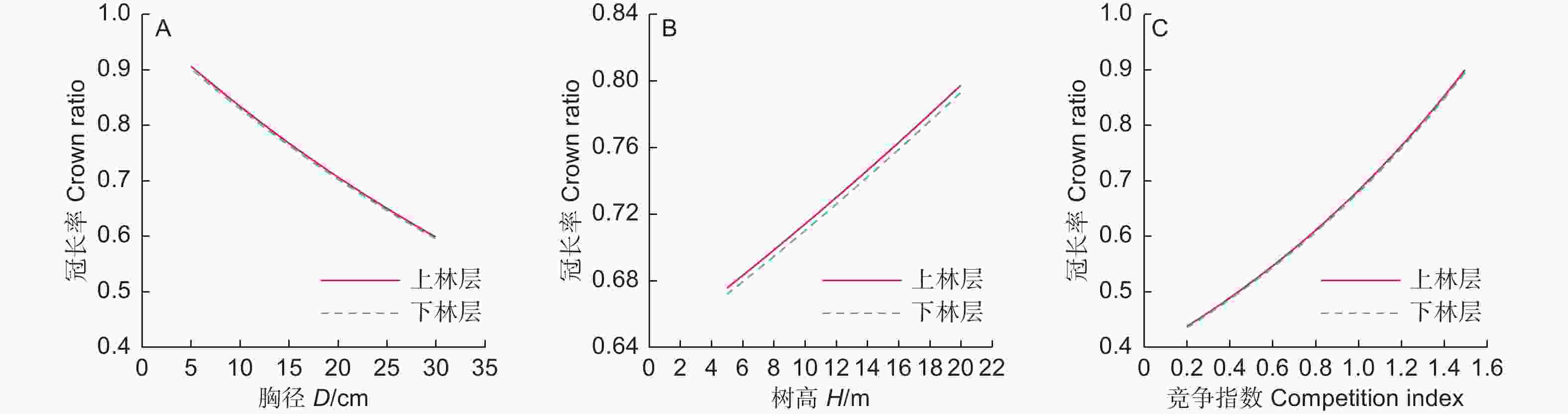
图2与图3分别对不同坡向与林层冠长率之间的差异进行了比较。由图2与图3可知，不同林层与不同坡向之间冠长率随胸径、竞争、树高变化曲线均呈现相似规律，即当其他条件相同时，阴坡冠长率大于半阳坡大于阳坡，上林层冠长率大于下林层冠长率。
-
不同学者在构建冠长率模型时最终选取的模型也不尽相同，如Fu等[17]采用逻辑斯蒂模型构建了黑龙江地区蒙古栎天然林单木冠长率模型；Li等[1]使用理查德模型构建了中国南方马尾松单木冠长率模型。本研究选取逻辑斯蒂模型、理查德模型、指数模型、威布尔模型共计4种模型的6种不同的形式进行比较最终选取基础模型。结果显示，指数模型形式的CR4拟合效果最好，理查德模型形式的CR2模型次之，有学者认为指数模型未能将冠长率预测值的范围限制在0～1之间，缺乏生物学意义[1]，也有学者提出在极端情况下，指数模型的预测值才会超出范围，应用指数模型可以得到有意义的结果[10]。本研究基于CR4模型的预测并未超出范围，因此将CR4模型作为基础模型。为探究不同林层及地形对冠长率的影响，本研究采用哑变量的方法将坡度、坡位、坡向加入到模型中，并选取对冠长率影响最大的地形因子，在其基础上进一步引入林层因子构建包含不同地形、林层的红松单木哑变量冠长率模型。结果显示坡向是对红松单木冠长率影响最大的地形因子，将坡向、林层作为哑变量加到模型中可以比较不同林层、坡向林木冠长率的差异[24]，与引入哑变量前的模型相比，R2a升高，RMSE降低，在一定程度上提升了模型的预估效果。
-
不同学者在构建冠长率模型时所引入的变量不同，但都综合考虑树木大小因子、竞争因子、地形因子以及林层因子[12,16-17]。本研究使用D、H来代表树木大小因子，通过再参数化方法引入Rd来代表竞争因子，通过哑变量的方法加入坡向和林层来代表地形与林层因子，与前人研究一致。胸径是森林调查时最易测得且最为精准的因子，本研究发现冠长率随着胸径的增大而减小，这与Holdaway的研究结果一致，Holdaway研究发现红松在年龄较小时冠长率随着胸径的增大而减小[25]。树高是预测冠长率的重要因子之一，以往的研究表明，冠长率随着树高的增大而减小[1,12,26]，在本研究中最终模型的树高参数虽为负值，但在冠长率随树高变化规律模拟中发现，不同Rd值下，冠长率呈现不同的变化规律。随着Rd的增大，冠长率随树高增长由负增长逐渐转变为正增长。这说明当树木本身竞争能力弱时，受到竞争木的影响较大，而树木竞争能力强时，竞争木对其的影响较小[27]，树高与冠长率之间达到平衡时可能代表植株为了应对相邻木的竞争而产生的适应机制[28]。竞争与林木冠长率的形成密切相关，郭孝玉[5]认为相邻木之间的竞争影响着树木整体的外貌形状，陈东升等[29]研究发现，竞争对树冠下部枝条影响较大，遗传因素对树冠上部枝条影响较大。本研究结果表明，冠长率随着相对直径的增大而增大，这说明树木本身竞争能力越强，所受竞争越小冠长率越大，与以往研究结果一致[12,30]。对不同坡向冠长率进行分析发现，阴坡冠长率大于半阳坡大于阳坡，这与郭明辉研究结果一致，郭明辉发现红松人工林阳坡红松单木生长率远低于阴坡，这是因为水分是红松生长最主要的限制因子，阳坡日照时数长温度高，土壤水分减少快，抑制了林木生长，而阴坡水分条件充足更适合红松生长[31-32]。对不同林层的冠长率进行分析发现，不同林层林木冠长率呈现相同的变化趋势，上林层冠长率大于下林层，原因可能是林分郁闭后，林木为了获取光资源而将资源用到高生长上，树冠顶部高度增加使林冠分层，下层林木竞争能力较弱，下部枝条受竞争木的影响较大，因此冠长率较小[29,33]。
-
本研究采用哑变量模型的方法，引入林木大小因子、竞争因子、地形因子与林层因子构建辽东山区红松人工林冠长率模型，探讨了不同林层、坡向下冠长率的差异以及冠长率随林木大小因子、竞争因子的变化规律，模型精度较高，能有效预估辽东山区红松人工林林木冠长率，可以为辽东山区红松人工林经营管理以及生长量预估提供参考。
Influencing Factors on the Crown Ratio of Korean Pine Plantation in Eastern Liaoning Province
- Received Date: 2022-03-20
- Accepted Date: 2022-06-19
- Available Online: 2022-12-20
Abstract:
DownLoad: